高三文科数学前三大题训练(有详解)VIP免费

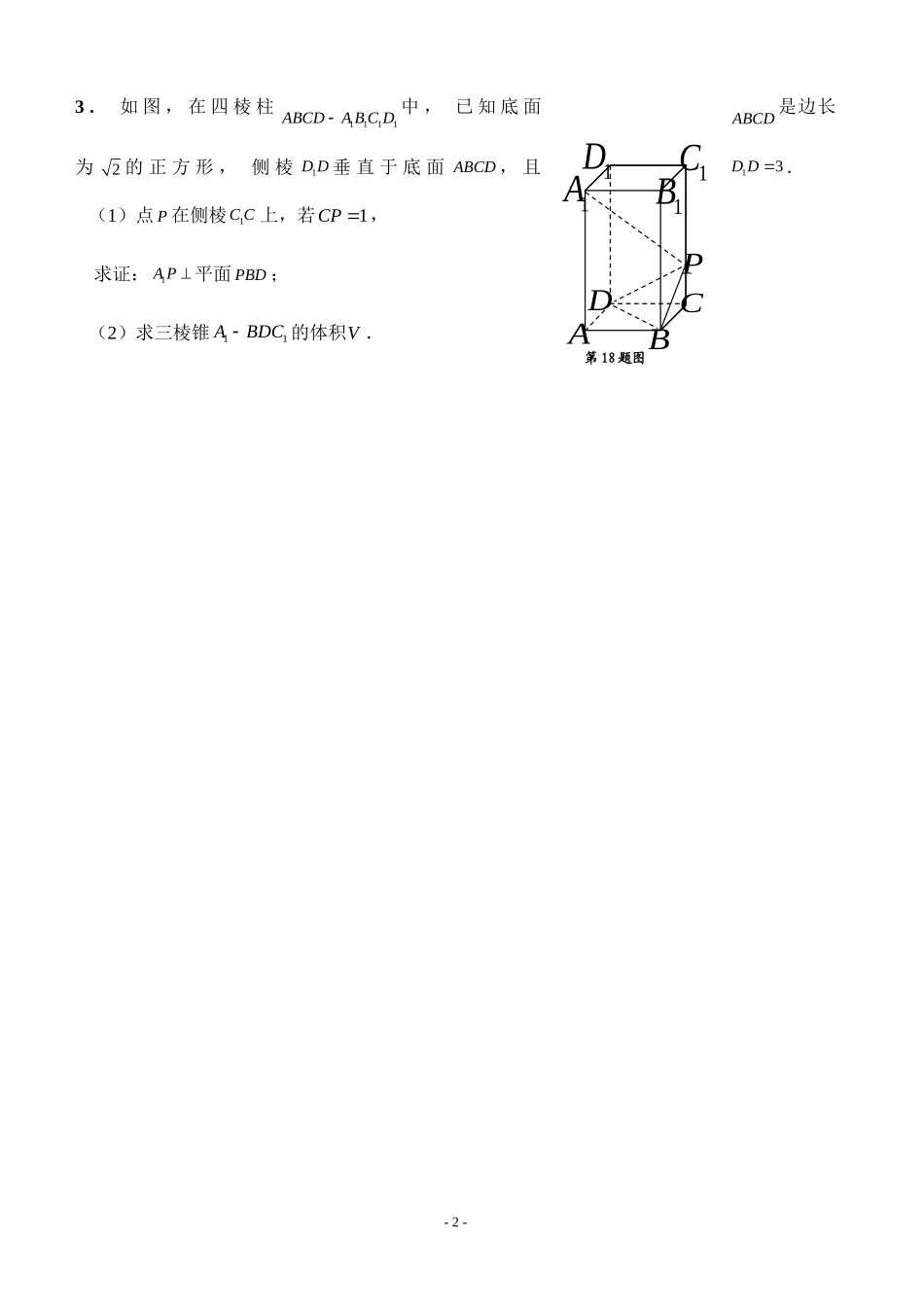
高三文科数学前三题训练1在平面直角坐标系xOy中，以Ox为始边，角的终边与单位圆O的交点B在第一象限，已知(1,3)A.（1）若OAOB,求tan的值.（2）若B点横坐标为45,求AOBS.2．市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车互不影响.假设李生早上需要先开车送小孩去丙地小学，再返回经甲地赶去乙地上班，（1）写出李生可能走的所有路线；（比如DDA表示走D路从甲到丙，再走D路回到甲，然后走A路到达乙）;（2）假设从甲到乙方向的道路B和从丙到甲方向的道路D道路拥堵，其它方向均通畅，但李生不知道相关信息，那么从出发到回到上班地没有遇到过拥堵的概率是多少？-1-第2题图C乙甲丙ABDEPABCD1A1B1C1D第18题图3．如图，在四棱柱1111ABCDABCD中，已知底面ABCD是边长为2的正方形，侧棱1DD垂直于底面ABCD，且13DD．（1）点P在侧棱1CC上，若1CP，求证：1AP平面PBD；（2）求三棱锥11ABDC的体积V．-2-12323371014754232甲乙4已知函数()sin()(0,0)fxx的一系列对应值如下表：x4064234y0112010（1）求()fx的解析式；（2）若在ABC中，2AC，3BC，1()2fA，求ABC的面积．5．（本题满分12分）某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示（1）求甲、乙两名运动员得分的中位数；（2）你认为哪位运动员的成绩更稳定？（3）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．（参考数据：2222222981026109466，236112136472222222）-3-6．（1）求证：EF⊥平面ABC；（2）求此三棱锥A—BCD的表面积；（3）若E、F分别是AC、AD上的中点，求点A到平面BEF的距离．-4-图3625x0611y11988967乙甲7已知函数2fxxx()sinsin.（1）求函数)(xfy的单调递增区间；（2）若243f()，求)42(f的值.8．（本小题满分12分）某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图3，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.（1）求x和y的值；（2）计算甲班7位学生成绩的方差2s；（3）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率.参考公式：方差2222121nsxxxxxxn，其中12nxxxxn.-5-侧视正视DCBAP图5图422229已知四棱锥PABCD的正视图是一个底边长为4、腰长为3的等腰三角形，图4、图5分别是四棱锥PABCD的侧视图和俯视图.（1）求证：ADPC；（2）求四棱锥PABCD的侧面PAB的面积.-6-高三文科数学前三题训练答案1．⑴解法1、由题可知：(1,3)A，(cos,sin)B，……1分(1,3)OA�，(cos,sin)OB�……2分OAOB，得0OAOB�……3分∴cos3sin0，1tan3……4分解法2、由题可知：(1,3)A，(cos,sin)B……1分3OAk，tanOBk……2分 OAOB，∴1OAOBKK……3分3tan1，得1tan3……4分解法3、设),(yxB，（列关于x、y的方程组2分，解方程组求得x、y的值1分，求正切1分）⑵解法1、由⑴22(1)(3)10OA，记AOx，(,)2∴3310sin1010，110cos1010（每式1分）……6分 1OB4cos5，得23sin1cos5（列式计算各1分）……8分3104103310sinsin()10510510AOB（列式计算各1分）……10分∴11310sin1012210AOBSAOBOAOB32（列式计算各1分）…12分解法2、由题意得：AO的直线方程为30xy……6分则23sin1cos5即43(,)55B（列式计算各1分）……8分则点B到直线AO的距离为4333555101010d（列式计算各1分）……10分又22(1)(3)10OA，∴1131031022102AOBSAOd（每式1分）…12分解法3、23sin1cos5即43(,)55B（每式1分）……6分即：(1,3)OA...