一元二次函数　课件　2VIP免费

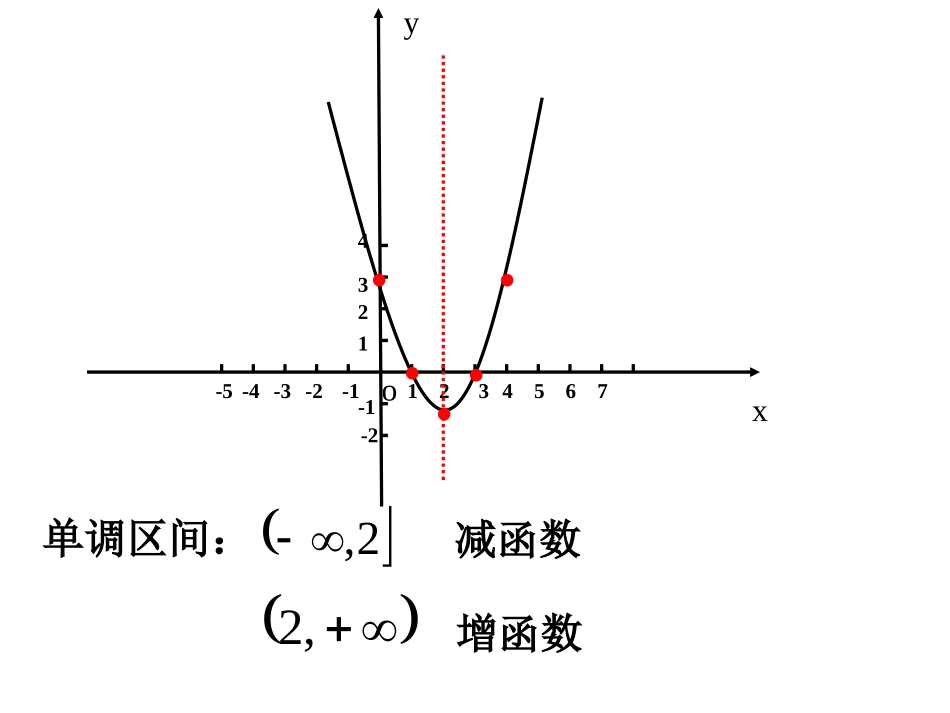
一元二次函数的单调性与最值高一数学组纽卡斯尔千禧桥单调性例1.作出函数f(x)=x2-4x+3的图像，并写出它单调区间及其在每一区间上的单调性。f(x)=x2-4x+3=(x-2)2-1对称轴：x=2顶点：（2，-1）单调区间：2,,2减函数增函数xoy1234567-1-2-3-4-51234-1-2.....变式：(1)判断函数f(x)=x2-4x+3在4,1上的单调性。(3)判断函数f(x)=x2-12x+35在4,1上的单调性。(2)判断函数f(x)=x2+4x+3在4,1上的单调性。xoy1234567-1-2-3-4-51234-1-2[]f(x)=x2-4x+3f(x)=x2-12x+35f(x)=x2+4x+3函数图像定义域单调性y=ax2+bx+c(a>0)Rdc,yxoab2ab2,,2abdab2cab2dabc2abc2,dab,2减函数增函数减函数减函数增函数增函数思考：类比上表讨论函数y=ax2+bx+c(a<0)的单调性?dc,dc,巩固练习：1.如果函数y=-5x2+mx+4在区间上是减函数1,在区间上是增函数,,1则m=____A.2B.-2C.10D.-102.若函数f(x)=x2-2(1-a)x+2在区间上为减函数4,则实数a的值得集合是__________3aaD例2.求函数f(x)=x2-4x+3的最小值。最值变式：(1)求函数f(x)=x2-4x+3在4,1上的最小值。(2)求函数f(x)=x2-12x+35在4,1上的最小值。(3)求函数f(x)=x2+4x+3在4,1上的最小值。xoy1234567-1-2-3-4-51234-1-2[]f(x)=x2-4x+3f(x)=x2-12x+35f(x)=x2+4x+3函数图像定义域最小值y=ax2+bx+c(a>0)Rdc,dab2cab2dabc2思考：类比上表讨论函数y=ax2+bx+c(a<0)的最大值?xoyab2)2(abf)(df)2(abf)(cf例3.求函数f(x)=x2+ax+4在区间上的最小值2,1xoy1234567-1-2-3-4-51234-1-22a2a2a课堂测试：1.已知函数f(x)=-x2+2x+8,那么______A.f(x)在上是减函数1,B.f(x)是减函数C.f(x)是增函数D.f(x)在上是增函数1,2.当时函数的值域为___5,0xcxxxf43)(2A.f(5)f(0),B.)32f(f(0),C.f(5)),32f(D.f(5)c,DC小结：1.一元二次函数在R及给定区间上的单调性与最值2.归纳，演绎，类比，数形结合（关键考察对称轴）引例奥运会的历史上，鲍勃比蒙在1968年的奥运会跳远比赛中跳出了令人惊叹的一跳。函数h(t)=4.6t-4.9t2(t的单位：s,h的单位：m)可以描述他跳跃时重心高度的变化。xoy13d567-1c-3-4-51234-1-2ab2ab2ab2xoy13d567-1c-3-4-51234-1-2ab2ab2ab2xoyab2思考：一元二次函数y=ax2+bx+c(a>0)的最小值情况如何？例2.求函数f(x)=x2-4x+3的最小值变式：求函数f(x)=x2-4x+3在，，1,24,15,4三个区间上的最小值。最值xoy1234567-1-2-3-4-51234-1-21,2最小值为f(1)=05,4最小值为f(4)=34,1最小值为f(2)=-1变式：判断函数f(x)=x2-4x+3在，，1,24,15,4三个区间上的单调性。思考：这三个区间有何特点？xoy1234567-1-2-3-4-51234-1-21,25,42,15,2减函数减函数增函数增函数xoy1234567-1-2-3-4-51234-1-2函数图像定义域单调性y=ax2+bx+c(a<0)Rdc,ab2,,2abdab2cab2dabc2abc2,dab,2xoyab2增函数减函数增函数增函数减函数减函数