空间向量与垂直关系VIP免费

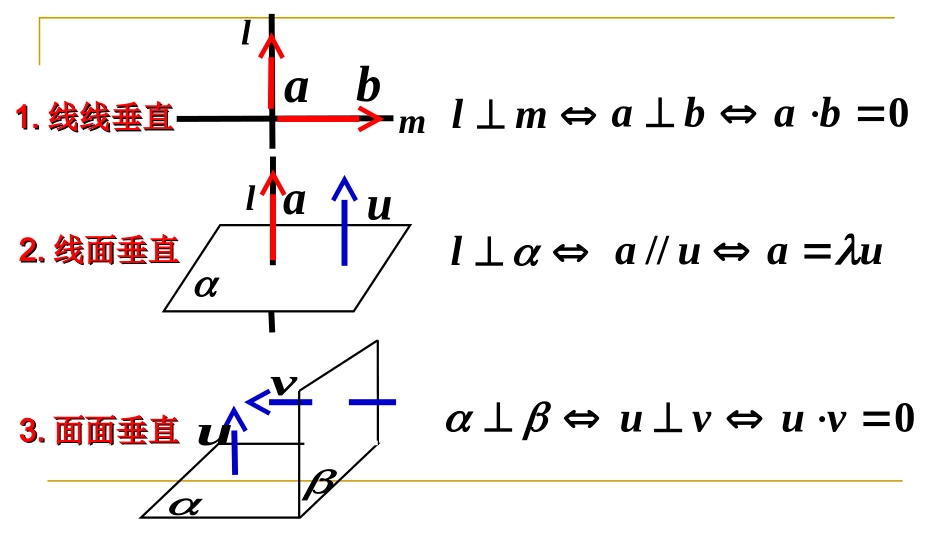
3.2.2空间向量与垂直关系设直线ml,的方向向量分别为ba,，平面,的法向量分别为vu,，则线线平行l∥ma∥bbka；线面平行l∥au0ua；面面平行∥u∥v.vku注意：1.这里的线线平行包括线线重合，线面平行包括线在面内，面面平行包括面面重合。ml0babamablluaua//ulauv0vuvu1.1.线线垂直线线垂直2.2.线面垂直线面垂直3.3.面面垂直面面垂直空间中垂直关系的向量表示线线垂直设直线l的方向向量为a＝(a1，a2，a3)，直线m的方向向量为b＝(b1，b2，b3)，则l⊥m⇔⇔线面垂直设直线l的方向向量是a＝(a1，b1，c1)，平面α的法向量是u＝(a2，b2，c2)，则l⊥α⇔⇔⇔(k∈R)面面垂直若平面α的法向量u＝(a1，b1，c1)，平面β的法向量v＝(a2，b2，c2)，则α⊥β⇔⇔＝0⇔a1a2＋b1b2＋c1c2＝0a1b1＋a2b2＋a3b3＝0(a1，b1，c1)＝k(a2，b2，c2)a·b＝0a＝kua∥uu·vu⊥v1.已知平面α的法向量为a＝(1,2，－2)，平面β的法向量为b＝(－2，－4，k)，若α⊥β，则k等于()A.5B.4C.－4D.－5D2.设直线l1，l2的方向向量分别为a＝(－2,2,1)，b＝(3，－2，m)，若l1⊥l2，则m等于()A.－2B.2C.6D.10D3.若直线l的方向向量为a＝(2,0,1)，平面α的法向量为n＝(－4,0,－2)，则直线l与平面α的位置关系为()A.l与α斜交B.l⊂αC.l∥αD.l⊥αD），，（），，（），，（），，（）法向量为（的一个单位），则平面，，（），，，（已知323231.323231.323231.323231.354122.4DCBAABCACAB..25111111BDAABCCDCBAABC平面。求证：的中点为，的所有棱长都为、如图所示，正三棱柱.12611111111CCAAAECBBEBBBCABBCABCBAABC平面证明：平面的中点。为，，，中，柱、如图所示，在直三棱