空间向量及其加减运算VIP免费

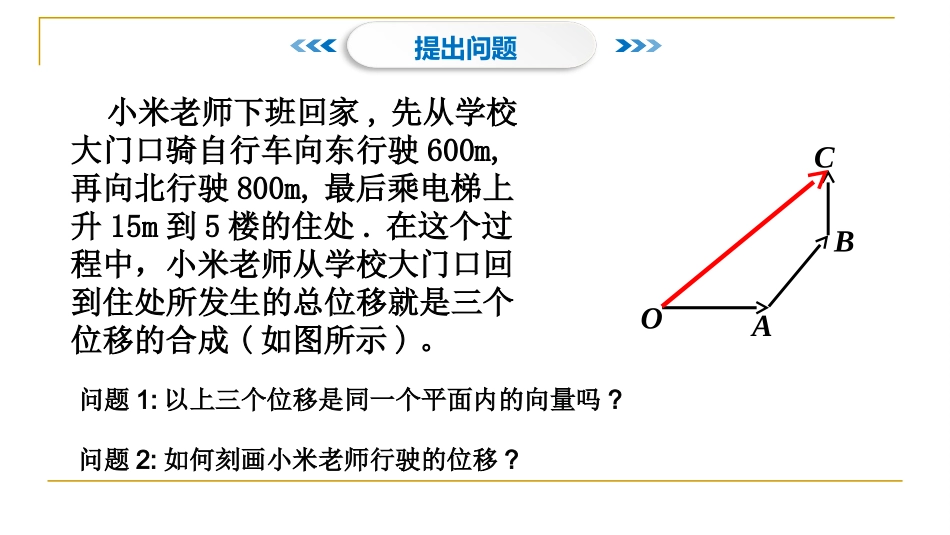
3.1.1空间向量及其加减运算问题1:以上三个位移是同一个平面内的向量吗?问题2:如何刻画小米老师行驶的位移?小米老师下班回家,先从学校大门口骑自行车向东行驶600m,再向北行驶800m,最后乘电梯上升15m到5楼的住处.在这个过程中，小米老师从学校大门口回到住处所发生的总位移就是三个位移的合成(如图所示)。OABC提出问题在必修4中，我们已经学习了平面向量，你还知道下列几个问题是怎么定义的吗？(1)什么叫向量？(2)什么是向量的长度(或模)?(3)什么叫零向量、单位向量、相反向量、相等向量？(4)向量的表示方法有哪些？那么，在空间中，上述问题又是如何定义的呢？启动思维【问题1】你能类比平面向量，填写空间向量的有关概念吗？内容平面向量空间向量定义画法及其表示模零向量单位向量相反向量相等向量在平面上，具有大小和方向的量在空间，具有大小和方向的量aAB�几何表示法字母表示法有向线段的长度表示向量的模，记为或aAB�aAB�几何表示法字母表示法长度为零的向量叫做零向量零向量的方向是任意的平面中模为1的向量空间中模为1的向量平面中长度相等，方向相反的两个向量空间中长度相等，方向相反的两个向量平面中方向相同且模相等的向量空间中方向相同且模相等的向量有向线段的长度表示向量的模，记为或aAB�长度为零的向量叫做零向量零向量的方向是任意的⑴5a且3bab.（）⑵空间中相反向量的模相等.（）⑶空间中任何一个向量与它的相反向量都不相等.（）⑷abab.（）⑸abab.（）⑹ab且bcac.（）⑺空间中任意两个单位向量必相等.（）⑻若两个空间向量相等，则它们的起点、终点相同.（）判断下列命题是否正确，若不正确，请说明理由：练一练abbabOABO′【问题2】空间两直线有异面关系，空间两向量是否也可能异面呢？结论：结论：1.1.空间任意两个向量都是共面向量，所以它们可用同一平面内的空间任意两个向量都是共面向量，所以它们可用同一平面内的两条有向线段表示。两条有向线段表示。2.2.因此凡是涉及空间任意两个向量的问题，平面向量中有关结论因此凡是涉及空间任意两个向量的问题，平面向量中有关结论仍适用于它们。仍适用于它们。空间任意两个向量都可以平移到同一平面内，成为一个平面内的两个向量.1.向量加法三角形法则:aAbBCbaaaAbBbOCba特点:首尾相接，首尾连特点:共起点babBaABAab�O特点：共起点，连终点，方向指向被减数2.向量加法平行四边形法则:3.向量减法三角形法则:空空间间向向量量的的加加减减法法空间向量的加法运算律:abcOABCab+abcOABCbc+ab+c+()ab+c+()abba交换律：）（）结合律：（cbacba空间向量加法的推广:（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；nnAAAAAAAA1433221（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量.nAA101A2A3A4A1nAnA1433221AAAAAAAAn1A2A3A4A1nAnA例1．在平行六面体（底面是平行四边形的四棱柱）ABCDABCD中，化简下列各表达式，并标出化简结果的向量：（1）ABBC�（2）ABADAA�（3）ABAAAD�ABCDA＇B＇C＇D＇结论：始点相同的三个不共面的向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量。''''1'2ABCDABCDABADCC�练习1.已知平行六面体，化简，并标出化简结果的向量：ABCDA＇B＇C＇D＇'''''''ABCDABCDABADAABDBC�练习2.已知平行六面体，用，，，表示向量和ABCDA＇B＇C＇D＇(1)()(2)()BABCBDAGABBC��练习练习33、、在空间四边形在空间四边形ABCDABCD中中,,化化简简AABBCCGGDDCGACAGBCABAG)(2）（BAGBBGBABDBCBA）（）（1平面向量概念加、减法运算运算律定义表示法相等向量减法:三角形法则加法:平行四边形法则或三角形法则空间向量)()(cbacbaabba加法交换律加法结合律小结类比方法数形结合思想零向量相反向量减法:三角形法则加法:平行四边形法则或三角形法则不共面的三个向量的和：平行六面体法则