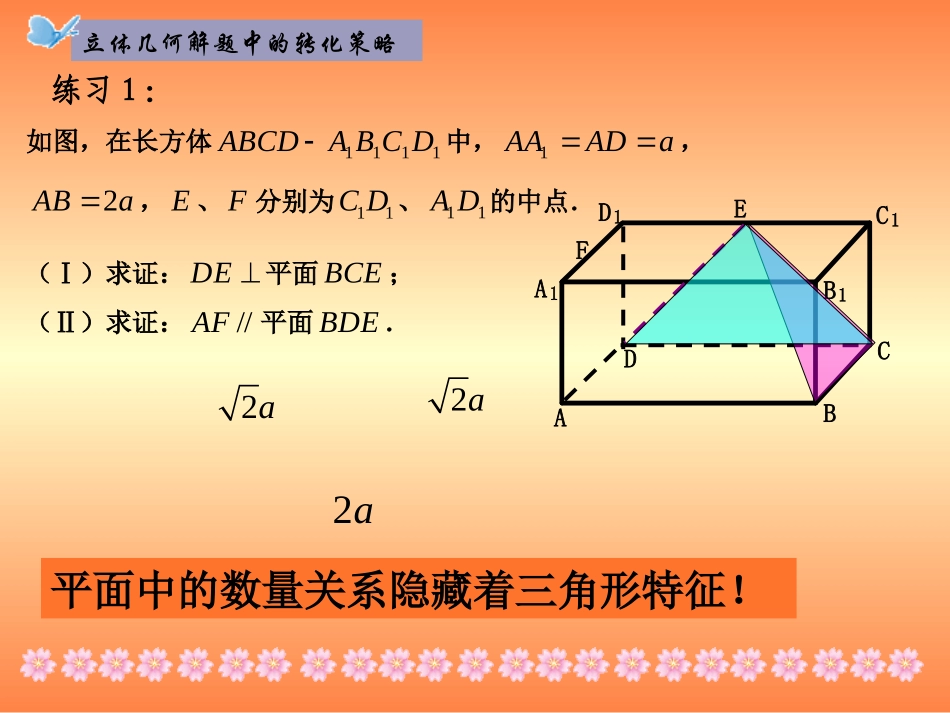
立体几何解题中的转化策略大策略:空间平面位置关系的相互转化小策略:③平行关系垂直关系①平行转化:线线平行线面平行面面平行②垂直转化:线线垂直线面垂直面面垂直如图,在长方体1111DCBAABCD中,aADAA1,aAB2,E、F分别为11CD、11DA的中点.(Ⅰ)求证:DE平面BCE;(Ⅱ)求证://AF平面BDE.立体几何解题中的转化策略练习1:D1C1B1A1DCBAEFD1C1B1A1DCBAEF如图,在长方体1111DCBAABCD中,aADAA1,aAB2,E、F分别为11CD、11DA的中点.(Ⅰ)求证:DE平面BCE;(Ⅱ)求证://AF平面BDE.立体几何解题中的转化策略平面中的数量关系隐藏着三角形特征!练习1:2a2a2aD1C1B1A1DCBAEF如图,在长方体1111DCBAABCD中,aADAA1,aAB2,E、F分别为11CD、11DA的中点.(Ⅰ)求证:DE平面BCE;(Ⅱ)求证://AF平面BDE.立体几何解题中的转化策略转化需要辅助线的添加!练习1:O策略:线面平行转化成线线平行(空间转化平面)ABCA1B1C1立体几何解题中的转化策略EF例1:在三棱柱111ABCABC中,1AA底面111ABC,且ABC是等边三角形,在侧面三条对角线111,,ABBCCA中,11ABBC,求证:11ABCAABCA1B1C1立体几何解题中的转化策略EF例1:在三棱柱111ABCABC中,1AA底面111ABC,且ABC是等边三角形,在侧面三条对角线111,,ABBCCA中,11ABBC,求证:11ABCA立体几何解题中的转化策略例2(综合题型):数学专业第5期备选题第4题如图,在矩形ABCD中,10AB,6BC,沿对角线BD把ABD折起,使A移到1A点,过点1A作1AO平面BCD,垂足O恰好在CD上(1)求证:1BCAD;(2)求证:平面1ABC平面1ABD;(3)求三棱锥1ABCD的体积.A1DCBAO关注翻折过程的“变”与“不变”!立体几何解题中的转化策略A1DCBAO题型三:平面图形与空间图形的相互转化题型三:平面图形与空间图形的相互转化例2(综合题型):数学专业第5期备选题第4题如图,在矩形ABCD中,10AB,6BC,沿对角线BD把ABD折起,使A移到1A点,过点1A作1AO平面BCD,垂足O恰好在CD上(1)求证:1BCAD;(2)求证:平面1ABC平面1ABD;(3)求三棱锥1ABCD的体积.关注翻折过程的“变”与“不变”!立体几何解题中的转化策略A1DCBAO例2(综合题型):数学专业第5期备选题第4题如图,在矩形ABCD中,10AB,6BC,沿对角线BD把ABD折起,使A移到1A点,过点1A作1AO平面BCD,垂足O恰好在CD上(1)求证:1BCAD;(2)求证:平面1ABC平面1ABD;(3)求三棱锥1ABCD的体积.关注翻折过程的“变”与“不变”!立体几何解题中的转化策略练习5:2007宁夏海南卷已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()A.34000cm3B.38000cm3C.32000cmD.34000cm2020正视图20侧视图1020俯视图10B立体几何解题中的转化策略一个多面体的直观图及三视图如图所示:例3(综合题型):,MNAFBC(其中分别是、的中点)正视图侧视图俯视图立体几何解题中的转化策略一个多面体的直观图及三视图如图所示:例3(综合题型):,MNAFBC(其中分别是、的中点)2ABADAEADEBCF直三棱柱ADAE22DECF(1)求该多面体的表面积与体积;策略:空间几何体的相互转化可考虑将该多面体补图成正方体221222222221242S212242V解:立体几何解题中的转化策略一个多面体的直观图及三视图如图所示:例3(综合题型):,MNAFBC(其中分别是、的中点)2ABADAEADEBCF直三棱柱ADAE22DECF//MNCDEF(2)求证:平面;策略:利用中位线将线面平行转化成线线平行BECMN在中,是中位线////MNECECCDEFMNCDEFMNCDEF平面平面平面BEECBEM连结,,则经过点解:立体几何解题中的转化策略一个多面体的直观图及三视图如图所示:例3(综合题型):,MNAFBC(其中分别是、的中点)2ABADAEADEBCF直三棱柱ADAE22DECF(3)求二面角CAFB的正切值;策略:将二面角转化成平面角,先找后求2,22,ABBFACCFMAF为的中点,MCMB连结--2,2,tan2CMBCAFBCBMBRtCMBCBCMBMB为二面角的平面角在中解:立体几何解题中的转化...