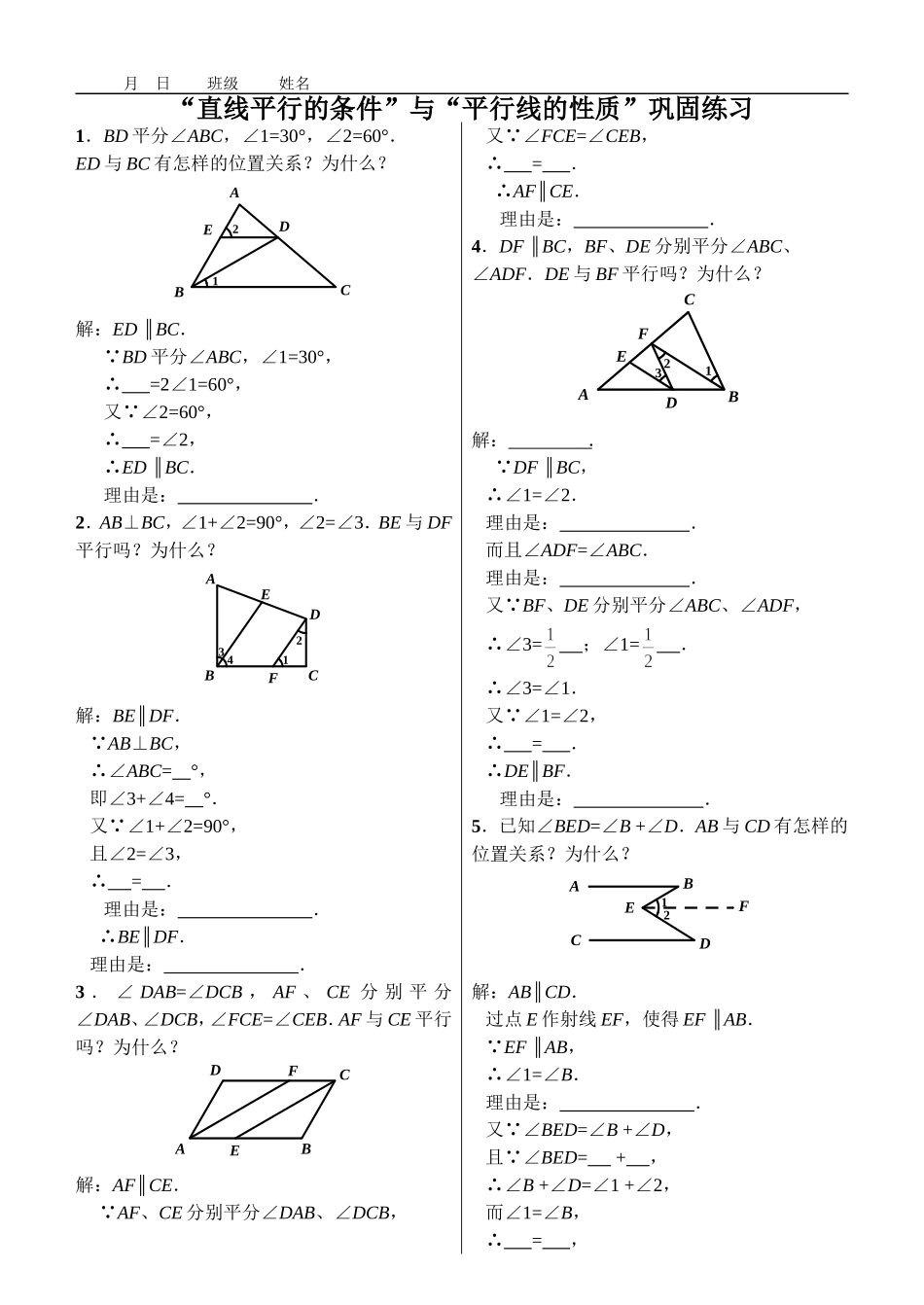
月日班级姓名“直线平行的条件”与“平行线的性质”巩固练习1.BD平分∠ABC,∠1=30°,∠2=60°.ED与BC有怎样的位置关系?为什么?2EDBC1A解:ED∥BC.∵BD平分∠ABC,∠1=30°,∴=2∠1=60°,又∵∠2=60°,∴=∠2,∴ED∥BC.理由是:.2.AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?4321EABCDF解:BE∥DF.∵AB⊥BC,∴∠ABC=°,即∠3+∠4=°.又∵∠1+∠2=90°,且∠2=∠3,∴=.理由是:.∴BE∥DF.理由是:.3.∠DAB=∠DCB,AF、CE分别平分∠DAB、∠DCB,∠FCE=∠CEB.AF与CE平行吗?为什么?FEDABC解:AF∥CE.∵AF、CE分别平分∠DAB、∠DCB,又∵∠FCE=∠CEB,∴=.∴AF∥CE.理由是:.4.DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?321EFABCD解:.∵DF∥BC,∴∠1=∠2.理由是:.而且∠ADF=∠ABC.理由是:.又∵BF、DE分别平分∠ABC、∠ADF,∴∠3=;∠1=.∴∠3=∠1.又∵∠1=∠2,∴=.∴DE∥BF.理由是:.5.已知∠BED=∠B+∠D.AB与CD有怎样的位置关系?为什么?21ABEDCF解:AB∥CD.过点E作射线EF,使得EF∥AB.∵EF∥AB,∴∠1=∠B.理由是:.又∵∠BED=∠B+∠D,且∵∠BED=+,∴∠B+∠D=∠1+∠2,而∠1=∠B,∴=,月日班级姓名∴∠FAB=;∠FCE=.又∵=,∴∠FAB=∠FCE.∴EF∥CD.理由是:.又∵EF∥AB,∴AB∥CD.“直线平行的条件”与“平行线的性质”巩固练习1.BD平分∠ABC,∠1=30°,∠2=60°.ED与BC有怎样的位置关系?为什么?2EDBC1A2.AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?4321EABCDF3.∠DAB=∠DCB,AF、CE分别平分∠DAB、∠DCB,∠FCE=∠CEB.AF与CE平行吗?为什么?4.DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?321EFABCD5.已知∠BED=∠B+∠D.AB与CD有怎样的位置关系?为什么?21ABEDCF月日班级姓名FEDABC