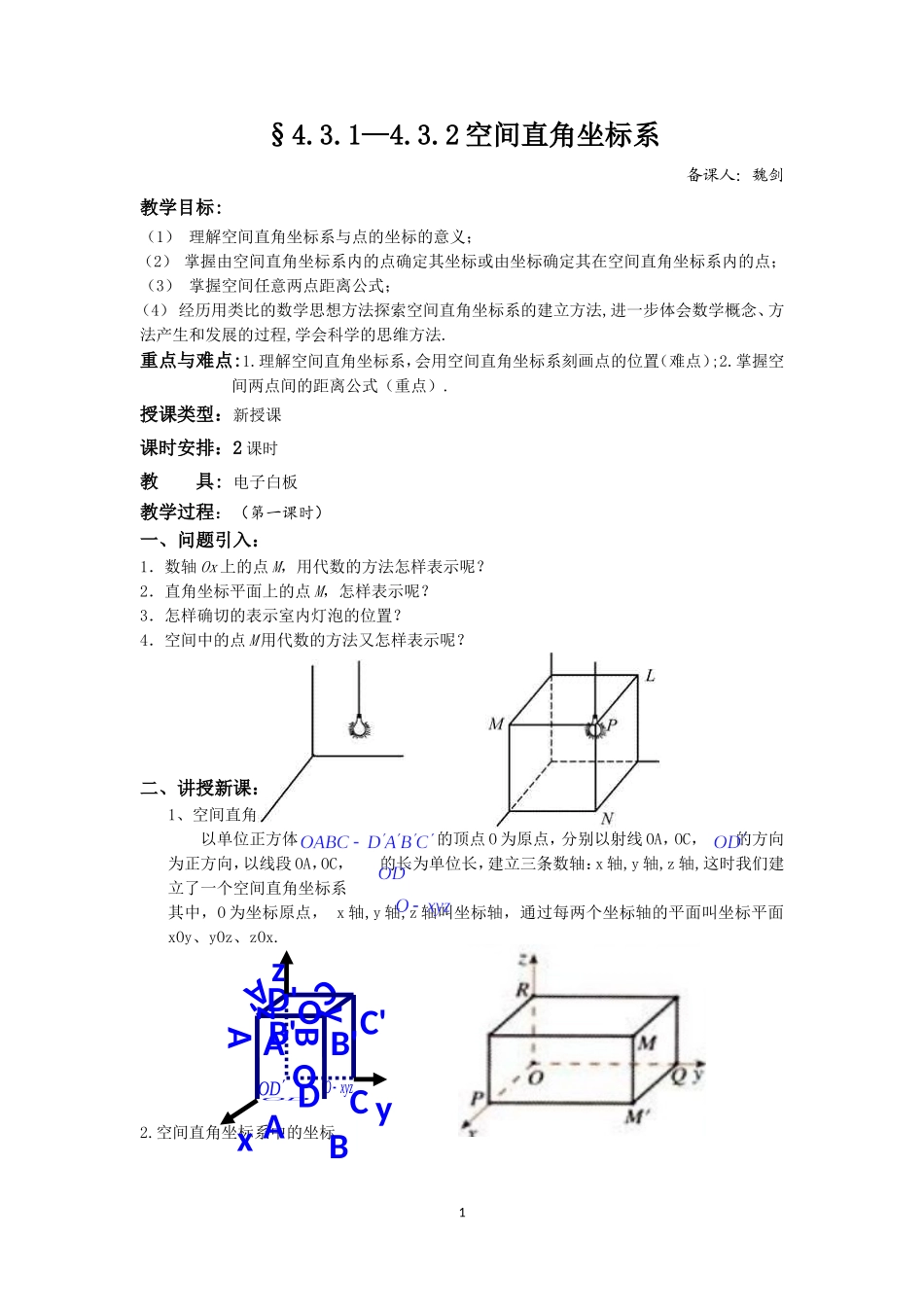
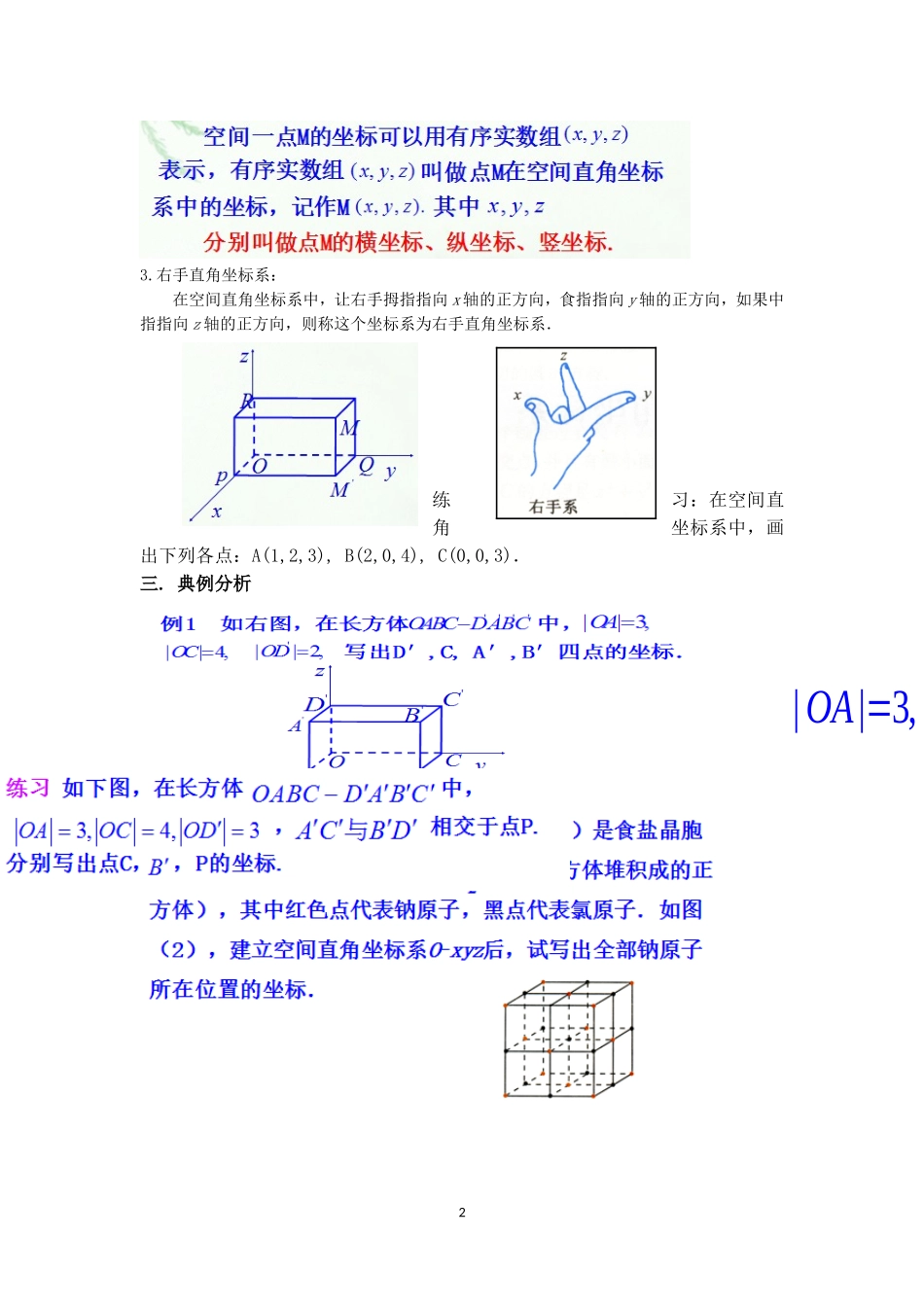
§4.3.1—4.3.2空间直角坐标系备课人:魏剑教学目标:(1)理解空间直角坐标系与点的坐标的意义;(2)掌握由空间直角坐标系内的点确定其坐标或由坐标确定其在空间直角坐标系内的点;(3)掌握空间任意两点距离公式;(4)经历用类比的数学思想方法探索空间直角坐标系的建立方法,进一步体会数学概念、方法产生和发展的过程,学会科学的思维方法.重点与难点:1.理解空间直角坐标系,会用空间直角坐标系刻画点的位置(难点);2.掌握空间两点间的距离公式(重点).授课类型:新授课课时安排:2课时教具:电子白板教学过程:(第一课时)一、问题引入:1.数轴Ox上的点M,用代数的方法怎样表示呢?2.直角坐标平面上的点M,怎样表示呢?3.怎样确切的表示室内灯泡的位置?4.空间中的点M用代数的方法又怎样表示呢?二、讲授新课:1、空间直角坐标系建立以单位正方体的顶点O为原点,分别以射线OA,OC,的方向为正方向,以线段OA,OC,的长为单位长,建立三条数轴:x轴,y轴,z轴,这时我们建立了一个空间直角坐标系其中,O为坐标原点,x轴,y轴,z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面xOy、yOz、zOx.2.空间直角坐标系中的坐标.1ODODOxyzD'B'A'COAByzC'D'B'A'COAByzx3.右手直角坐标系:在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.练习:在空间直角坐标系中,画出下列各点:A(1,2,3),B(2,0,4),C(0,0,3).三.典例分析2||3,OA四.探究:1.体会在坐标轴上、在坐标平面xOy,yOz,xOz内的点其坐标的特征2.点的对称问题(关于轴,关于原点,关于坐标平面)3.空间中点坐标公式.五.课堂练习1.点M(2,-3,1)关于坐标原点的对称点是____________.2.在空间直角坐标系中,若点B是点A(1,2,3)在坐标平面yOz内的射影,则OB的长度为______.3.以棱长为1的正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线为坐标轴,建立空间直角坐标系,则面AA1B1B对角线交点的坐标为_________.六.课堂小结1、空间直角坐标系2、空间直角坐标系中点和坐标的关系3、应用(第二课时)一.新课引入建筑用砖通常是长方体,我们可以拿尺子测量出一块砖的长、宽和高,那么怎样测量它的对角线AC′的长度呢?直接测量比较困难,我们可以用间接的方法去测量。如果有三块砖,你如何测量AC′的长度,两块呢?二.新课讲授1.思考:类比平面两点间的距离公式的推导,在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的距离,怎么求?(1)先看简单的情形空间中任意一点的坐标到原点之间的距离公式会是怎样呢?3(,,)Pxyz探究:如果是定长r,那么表示什么图形?(2)如果是空间中任意一点到点之间的距离公式会是怎样呢?结论:(1)空间任意一点到原点的距离:(2)空间任意两点间的距离:三.典例分析:练习:1.求下列两点的距离例2.在z轴上求与两点A(4,1,7)和B(3,5,2)等距离的点.练习:1.在z轴上求一点M,使点M到A(1,0,2)与点B(1,-3,1)的距离相等.四.课堂练习:五.课堂小结:1、会画空间直角坐标系;2、已知点写出其空间直角坐标;4OP2222xyzr1111(,,)Pxyz2222(,,)Pxyz3、空间直角坐标系中距离公式.六.课后作业:《创新设计》4.3.1—4.3.2七.教学反思:5