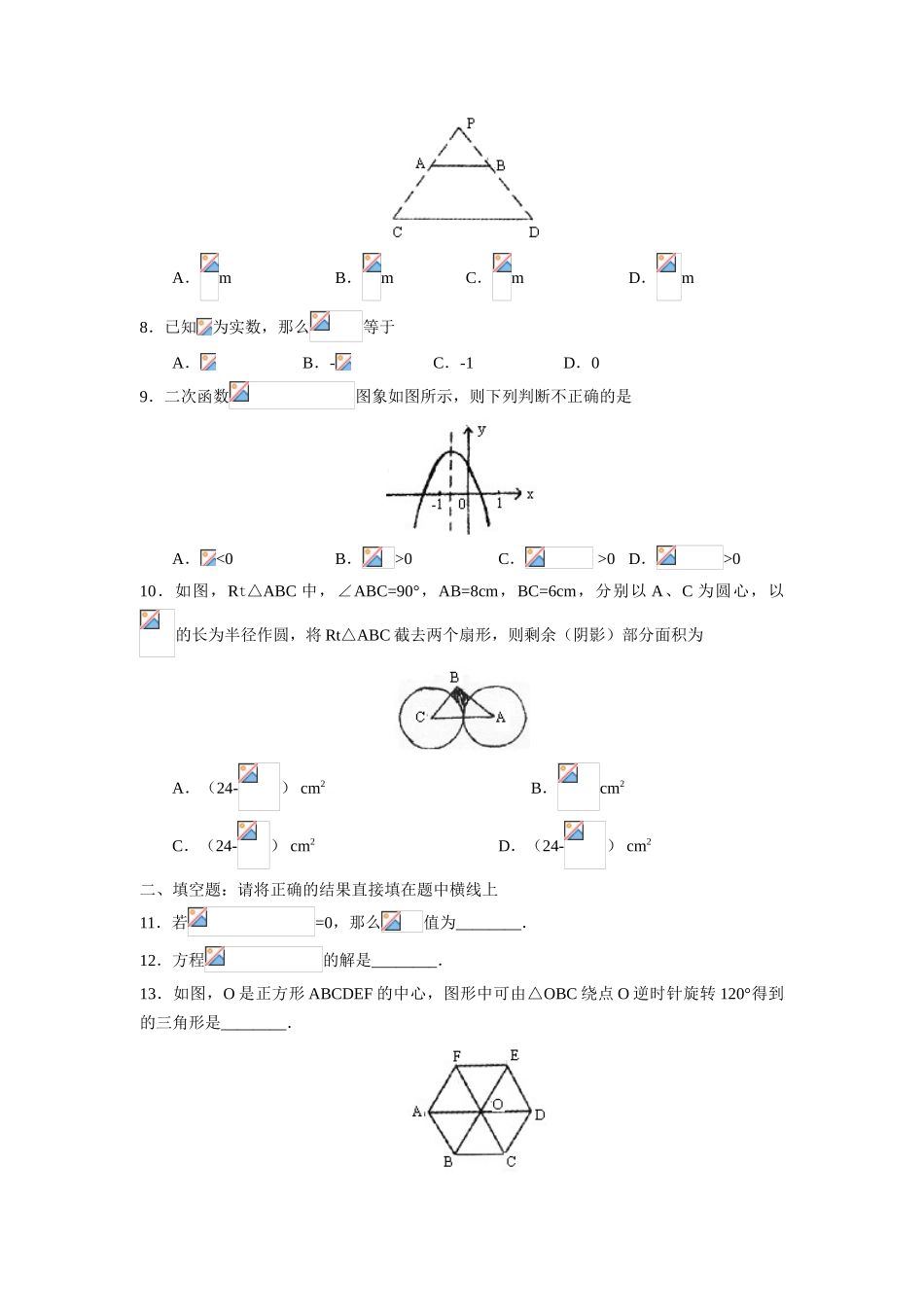
福建省永春一中2020九年级期末考试数学试卷一、选择题:在下列各题所给出的四个选项中,只有一个是正确的,请将正确选项的代号填在下列答题框内。1.下列计算正确的是A.B.C.D.=±32.已知=2是一元二次方程=0的一个解,则m的值是A.-3B.3C.0D.0或33.视力表对我们来说并不陌生。如图是视力表的一部分,其中开口向上的两个“E”之间的变换是A.平移B.旋转C.对称D.位似4.如图所示,给出下列条件:①∠B=∠ACD②∠ADC=∠ACB③④,其中单独能判定△ABC∽A△CD的个数为A.1个B.2个C.3个D.4个5.已知⊙O1和⊙O2相切,⊙O1直径为9cm,⊙O2直径为4cm,则O1O2长为A.5cm或13cmB.2.5cmC.6.5cmD.2.5cm或6.5cm6.下列事件中,必然事件是A.抛掷1个均匀搬子,出现6点向上B.两直线被第三条直线所截,同位角相等C.366人中至少有2人的生日相同D.实数的绝对值是非负数。7.如图,电灯P在横杆AB正上方,AB在灯光下影子长为CD,AB//CDAB=2m,CD=5m,点P到CD距离为3m,则P到AB距离是A.mB.mC.mD.m8.已知为实数,那么等于A.B.-C.-1D.09.二次函数图象如图所示,则下列判断不正确的是A.<0B.>0C.>0D.>010.如图,Rt△ABC中,∠ABC=90°,AB=8cm,BC=6cm,分别以A、C为圆心,以的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分面积为A.(24-)cm2B.cm2C.(24-)cm2D.(24-)cm2二、填空题:请将正确的结果直接填在题中横线上11.若=0,那么值为________.12.方程的解是________.13.如图,O是正方形ABCDEF的中心,图形中可由△OBC绕点O逆时针旋转120°得到的三角形是________.14.半径为5的⊙O内,弦AB长6,则圆心到弦AB距离为________.15.若圆锥母线长3cm,底面周长47πcm,则其侧面展开图面积为________.16.袋中装有10个大小、质地相同的红球、白球,任意摸出一球为红球概率为,则袋中白球________个.17.抛物线顶点坐标________,对称轴直线=________18.抛物线向上平移1个单位,所得抛物线解析式为________19.如图△ABC与△A’B’C’是位似图形,点O为位似中心,若OA=2AA’,S△ABC=8,则S△A’B’C’=________.20.如图所示,桥拱是抛物线形,其函数关系式为,当水位线在AB位置时,水面宽12m。这时水面离桥顶高度为________m三、解答题:本大题共6小题。21.某商场今年“十一”期间举行购物摸奖活动,摸奖箱里有四个标号分别为1,2,3,4的质地,大小都相同的小球,任意摸出一个小球,记下小球标号后,放回箱里并摇匀,再摸出一个小球,再记下小球标号。商场规定:两次摸出的小球之和为“8”或“6”时才算中奖。请结合“树形图法”或“列表法”,求出顾客小彦参加此次摸奖活动时中奖的概率。22.如图,在10×10正方形网格中,每个小正方形边长均为1个单位。建立坐标系后,△ABC中点C坐标为(0,1).(1)把△ABC绕点C顺时针旋转90°后得到△A1B1C1,画出△A1B1C1,并写出A1坐标。(2)把△ABC以O为位似中心放大,使放大前后对应边长为1:2,画出放大后的△A2B2C2,并写出A2坐标。23.汽车产业的发展,有效促进我国现代建设。某汽车销售公司2007年盈利3000万元,到2009年盈利4320万元,且从2007年到2009年,每年盈利的年增长率相同,该公司2008年盈利多少万元?24.如图,某班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度25.如图,AB为半圆O的直径,点C在半圆上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC(1)求证:AD是半圆O的切线;(2)求证:△ABC∽△DOA;(3)若BC=2,CE=,求AD的长。26.某水产品养殖企业为指导该企业某种产品的养殖和销售,对历年市场行情和水产品的养殖情况进行了调查。调查发现这种水产品的每千克售价(元)与销售月份(月)满足关系式+36,而其每千克成本(元)与销售月份(月)满足的函数关系如图所示:(1)试确定、的值;(2)求出这种水产品每千克的利润(元)与销售月份(月)之间的函数关系式;(3)几月份出售这种水产品每千克利润最大?最大利润是多少?九...