正弦定理课件 (2)VIP免费

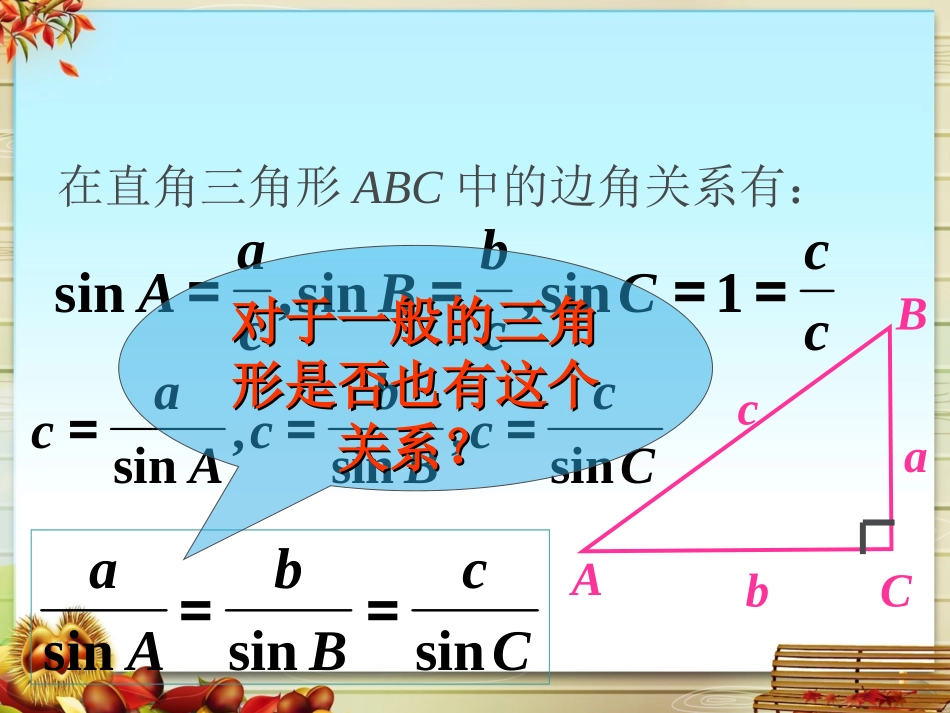
1.问题的引入:.在我国古代就有嫦娥奔月的神话故事.明月高悬,我们仰望夜空,会有无限遐想,不禁会问,月亮离我们地球有多远呢?科学家们是怎样测出来的呢？我们这一节所学习的内容就是解决这些问题的有力工具.ABCabc在直角三角形ABC中的边角关系有：ccCcbBcaA====1sin,sin,sinCccBbcAacsin,sin,sin===CcBbAasinsinsin==对于一般的三角对于一般的三角形是否也有这个形是否也有这个关系？关系？bADcADCBsin,sin所以AD=csinB=bsinC,即,sinsinCcBb同理可得,sinsinCcAaDAcbCB图1过点A作ADBC⊥于D,此时有若三角形是锐角三角形,如图1,＝＝aasinsinCCCCbADsinsin）（且仿(2)可得D若三角形是钝角三角形,且角C是钝角如图2,此时也有cADBsin交BC延长线于D,过点A作ADBC⊥，CAcbB图2CcBbAasinsinsin：在一个三角形中各边和它所对角的正弦的比相等.＝正弦定理＝＝aasinsinCC？＝＝asinAbsinBcsinC＝2R.=2RbsinBB`ABCbOABCbOB`ABCbO（R为△ABC外接圆半径）CcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即含三角形的三边及三内角,由己知二角一边或二边一角可表示其它的边和角定理结构特征:剖析定理、加深理解剖析定理、加深理解1、A+B+C=π2、大角对大边，大边对大角正弦定理：CcBbAasinsinsin剖析定理、加深理解3、正弦定理可以解决三角形中的问题：①已知两角和一边，求其他角和边②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角正弦定理：CcBbAasinsinsin剖析定理、加深理解4、一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形正弦定理：CcBbAasinsinsin定理的应用例1：在△ABC中，已知c=10,A=45。,C=30。，解三角形.（即求出其它边和角）解：B180(AC)105sinsinbcBC由正弦定理得b=CBcsinsin=30sin105sin10（1）已知两角和任一边，求其他两边和一角sinsinacAC由正弦定理sinsincAaC得=21030sin45sin10BACbc)26(5a根据三角形内角和定理，(2)已知两边和其中一边的对角,求其他边和角.（三角形中大边对大角）例2根据下列条件解三角形：(1)b＝√2，c＝√3，B＝45º；(2)b＝2，c＝√2，B＝45º．小结2.正弦定理可解以下两种类型的三角形：（1）已知两角及一边；(只有一解)（2）已知两边及其中一边的对角→↓.1.正弦定理是解斜三角形的工具之一.＝2R解三角形时，注意大边对大角CcBbAasinsinsin如在△ABC中，已知a，b和角A时，解的情况如下：A为锐角A为钝角或直角图形A为锐角A为钝角或直角关系式a＝bsinAbsinA＜a＜ba≥ba＞b解的个数一解两解一解一解课后探究:作业：P101，2：你还可以用其它方法证明正弦定理吗？