单调性与最大（小）值2VIP免费

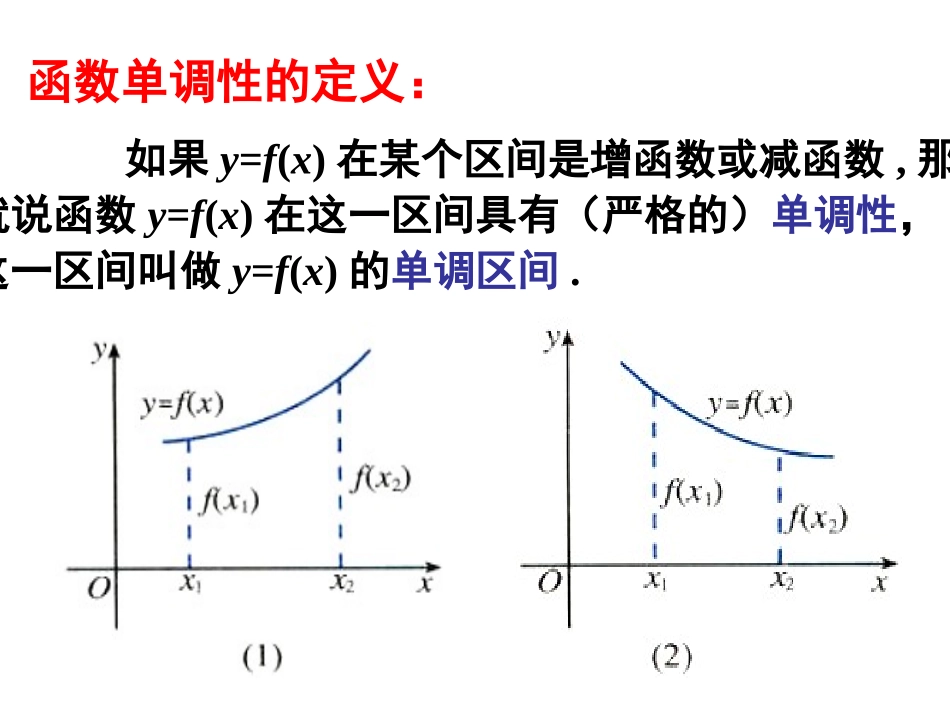
1.3.1单调性与最大（小）值（2）).()()),()()(()(,:)(21212121减函数上是增函数在区间那么就说函数时，都有，当值上的任意两个自变量的内某个区间如果对于定义域的定义域为一般地，设函数DxfxfxfxfxfxxxxDIIxf定义:复习提问如果y=f(x)在某个区间是增函数或减函数,那么就说函数y=f(x)在这一区间具有（严格的）单调性，这一区间叫做y=f(x)的单调区间.函数单调性的定义：证明函数单调性的方法步骤1.任取x1，x2∈D，且x10,于是(x1-1)(x2-1)>0,12()()fxfx即故当x=2时，max2y；当x=6时，min0.4.y设x1,x2∈[2,6]，12,(0),xx，+12121211()()()()fxfxxxxx121211()()xxxx120,xx解：则211212()xxxxxx12121()(1)xxxx1212121()()xxxxxx120,xx12()()0fxfx，12()()fxfx1()(0,1]fxxx在上是减函数.即1201xx，例3.求函数的最值.1()(0)fxxxx12xx且，设①当0