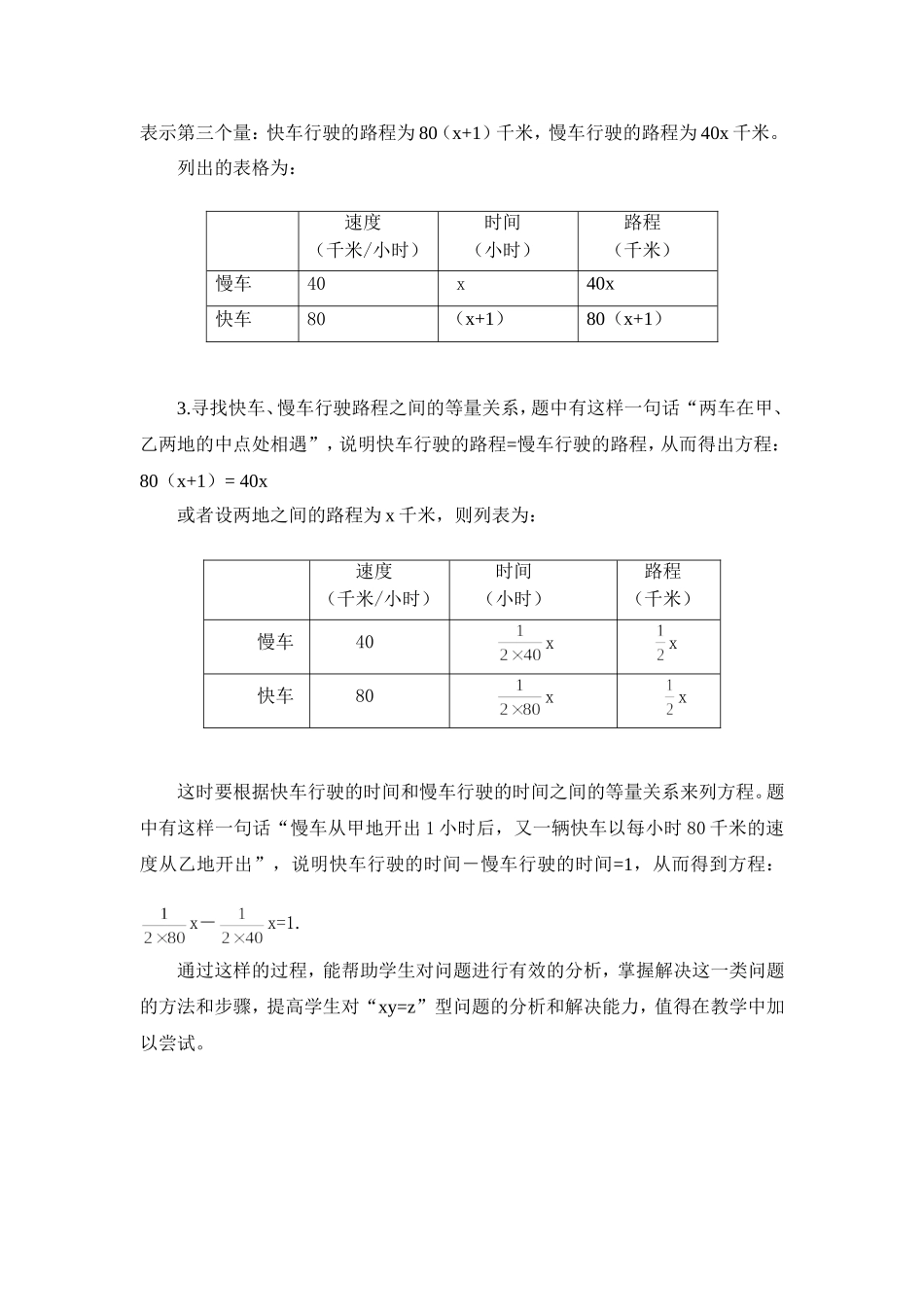
浅谈用方程解决“xy=z”问题中的难点突破赵玉霞用方程解决问题是初中数学的难点,也是教师普遍感觉比较难讲的一个单元而这里的难点中的难点当要数等量关系的寻找了。如何来突破难点,而不是就题论题,通过一个问题的解决来说透一类问题呢?我认为可以分为下面几个步骤和方法:1.弄清实际问题中的基本量及其关系目前我们遇到的问题类型中最多就是路程问题、工作问题、销售问题等,而这类问题都有非常明确的基本量和基本关系。如:(1)路程问题:速度×时间=路程(2)工作问题:工作效率×工作时间=工作量(3)销售问题:销售单价×销售量=销售额它们都是形如“xy=z”型的问题。2.列表分析问题中的基本量。(1)先找已知量(2)再找要求的量,用未知数表示,并用未知数表示相关的量(3)然后用前两个量把第三个量表示出来3.寻找第三个量之间的等量关系,列出方程。举例说明:一辆慢车从甲地开出1小时后,又一辆快车以每小时80千米的速度从乙地开出,若干小时后,两车在甲、乙两地的中点处相遇,已知慢车速度是快车速度的,求相遇时慢车走了多少小时?甲、乙两地的路程是多少千米?分析:1.这是一个路程问题:速度×时间=路程。因此这里要分析的是快车的速度、慢车的速度、快车行驶的时间和慢车行驶的时间、快车行驶的路程和慢车行驶的路程。2.已知量:快车的速度=80千米/小时,慢车的速度=40千米/小时要求的量有两个:一个是时间,一个是总路程,因此这里设未知数可以考虑两种设法。一个是设慢车行驶的时间,还可以设总路程。我们以设时间为例。设慢车走了x小时两车相遇,则快车行驶的时间就是(x+1)小时。镇江市实验初级中学第三届教育教学论文评选表示第三个量:快车行驶的路程为80(x+1)千米,慢车行驶的路程为40x千米。列出的表格为:3.寻找快车、慢车行驶路程之间的等量关系,题中有这样一句话“两车在甲、乙两地的中点处相遇”,说明快车行驶的路程=慢车行驶的路程,从而得出方程:80(x+1)=40x或者设两地之间的路程为x千米,则列表为:这时要根据快车行驶的时间和慢车行驶的时间之间的等量关系来列方程。题中有这样一句话“慢车从甲地开出1小时后,又一辆快车以每小时80千米的速度从乙地开出”,说明快车行驶的时间-慢车行驶的时间=1,从而得到方程:x-x=1.通过这样的过程,能帮助学生对问题进行有效的分析,掌握解决这一类问题的方法和步骤,提高学生对“xy=z”型问题的分析和解决能力,值得在教学中加以尝试。速度(千米/小时)时间(小时)路程(千米)慢车40x40x快车80(x+1)80(x+1)速度(千米/小时)时间(小时)路程(千米)慢车40xx快车80xx