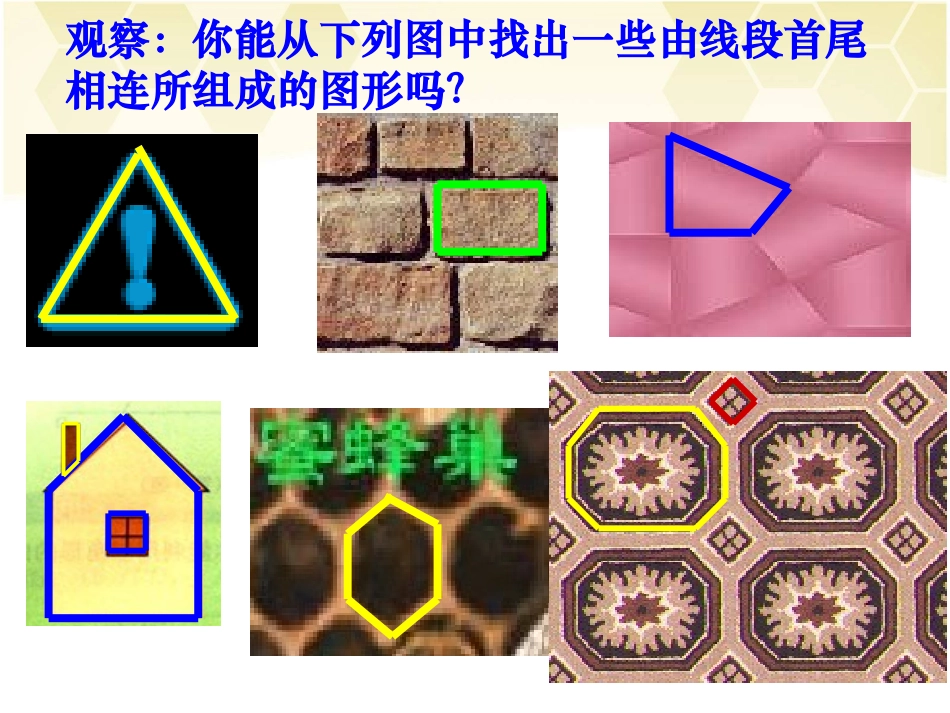
第2章四边形2.1多边形第1课时多边形的内角观察:你能从下列图中找出一些由线段首尾相连所组成的图形吗?多边形的有关概念:在平面内,由一些线段首尾顺次相接组成的图形叫多边形.组成多边形的各条线段叫作多边形的边.相邻两条边的公共端点叫作多边形的顶点.连接不相邻的两个顶点的线段叫作多边形的对角线.相邻两边组成的角叫作多边形的内角,简称多边形的角.例如在图中,AB是边,E是顶点,BD是对角线,∠A是内角.多边形根据边数可以分为三角形,四边形,五边形,······在平面内,边相等、角也都相等的多边形叫作正多边形.三角形的内角和等于180°,四边形的内角和是多少度呢?动脑筋如图,四边形ABCD的一条对角线AC把它分成两个三角形,因此四边形的内角和等于这两个三角形的内角和,即180°×2=360°.探究在下列各个多边形中,任取一个顶点,通过该顶点画出所有的对角线,并完成下表.图形边数可分成三角形的个数多边形的内角和五边形53(5-2)×180°六边形64(6-2)×180°七边形75(7-2)×180°八边形86(8-2)×180°···············n边形nn-2(n-2)×180°如图,n边形共有n个顶点A1,A2,A3,···An.与顶点A1不相邻的顶点有(n-3)个,因此从顶点A1出发有(n-3)条对角线,n边形的内角和等于这(n-2)个三角形的内角和,即(n-2)·180°.由此得到:n边形的内角和等于(n-2)·180°.你还可以用其他方法探究n边形的内角和公式吗?如图,在n边形内任取一点O,与多边形各顶点连接,把n边形分成n个三角形,用n个三角形的内角和n·180°减去中心的周角360°,得n边形的内角和(n-2)·180°.动脑筋例(1)十边形的内角和是多少度?(2)一个多边形的内角和等于1980°,它是几边形?解:(1)十边形的内角和是(10-2)·180°.=1440°.(2)设这个多边形的边数为n,则(n-2)·180°=1980°.解得n=13.所以这是一个十三边形.例题例题练习1.(1)正十二边形每一个内角是多少度?解:(1)十边形的内角和是(12-2)·180°.=1800°.(2)一个多边形的内角和等于1800°,它是几边形?解:设这个多边形的边数为n,则(n-2)·180°=1800°.解得n=12.答:它是十二边形.练习2.过多边形某个顶点的所有对角线,将这个多边形分成10个三角形,那么这个多边形是几边形?解:这个多边形的边数为10+2=12(条)答:这个多边形是十二边形.多边形内角和n边形的内角和等于(n-2)·180°.课堂小结: