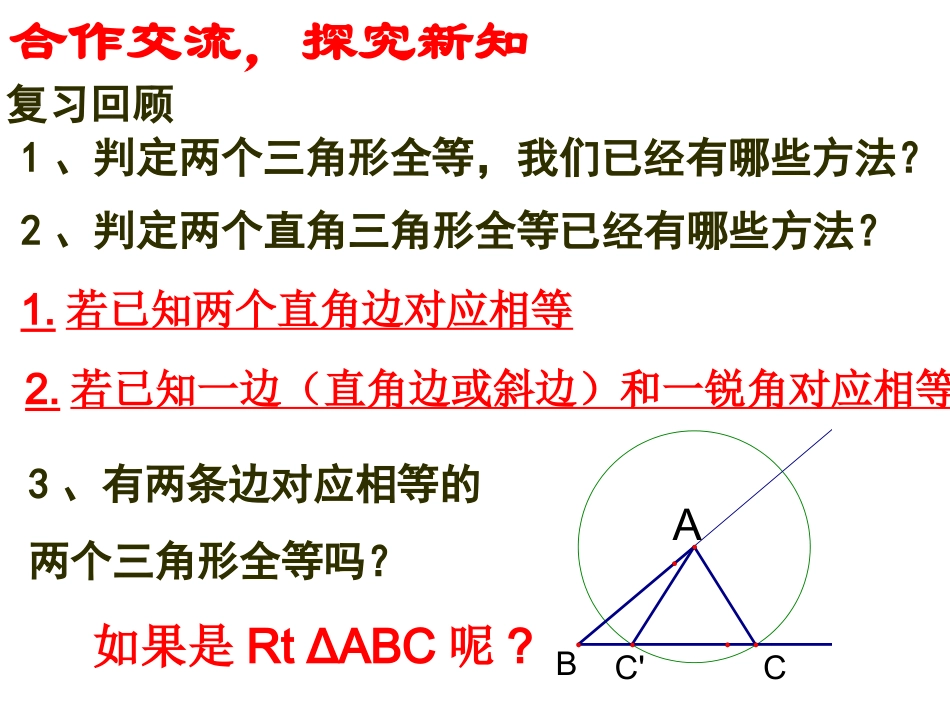
2.8直角三角形的全等的判定复习回顾1、判定两个三角形全等,我们已经有哪些方法?2、判定两个直角三角形全等已经有哪些方法?合作交流,探究新知1.若已知两个直角边对应相等2.若已知一边(直角边或斜边)和一锐角对应相等3、有两条边对应相等的两个三角形全等吗?C'CBA如果是RtΔABC呢?思考问题,探索结论已知线段a=3cm,c=5cm,用直尺和圆规作RtΔABC,使∠C=Rt,BC=a,AB=c∠请比较你和同桌的图形,有什么发现吗?证明结论斜边和一条直角边对应相等的两个三角形全等吗?如图在ΔABC和ΔA′B′C′中,∠C=∠C′=Rt∠,AB=A′B′,AC=A′C′,说明ΔABC和ΔA′B′C′全等的理由。B’斜边和一条直角边对应相等的两个直角三角形全等.简写:“斜边、直角边”或“HL”AB=A´B´AC=A´C´(或BC=B´C´)B'C'A'ACB∴RtABCRtA´B´C´(HL)△≌△直角三角形全等的判定方法:∵在RtABC△和RtA´B´C´△中几何语言:几何语言:如图,已知∠ACB=∠BDA=900,要使△ABC≌△BDA,还需要增加一个什么条件?把它们分别写出来.增加AC=BD;ABCD增加BC=AD;增加∠ABC=BAD∠;增加∠CAB=DBA∠;角平分线性质:角平分线上的点到角的两边距离相等。温故知新21PEDO反之成立吗?角的内部,到角两边距离相等的点,是否一定在这个角的平分线上?角平分线性质:角平分线上的点到角的两边距离相等。想一想21PEDO反之成立吗?角的内部,到角两边距离相等的点,是否一定在这个角的平分线上?已知P是∠DOE内部一点,PD⊥OD,PE⊥OE,D、E分别是垂足,且PD=PE,则点P在∠AOB的平分线上。请说明理由。角平分线性质:角平分线上的点到角的两边距离相等。21PEDO角平分线判定:角的内部,到角两边距离相等的点,在这个角的平分线上。∵∠1=∠2,PD⊥OD,PE⊥OE,∴PD=PE∵PD⊥OD,PE⊥OE,PD=PE∴∠1=∠2提高题提高题如图所示,在△ABC中,一边BC的中垂线与∠BAC的平分线交于点D,DEAB⊥,DFAC⊥,垂足分别为E和F,则BE=CF,并说明理由。ABCDFGE