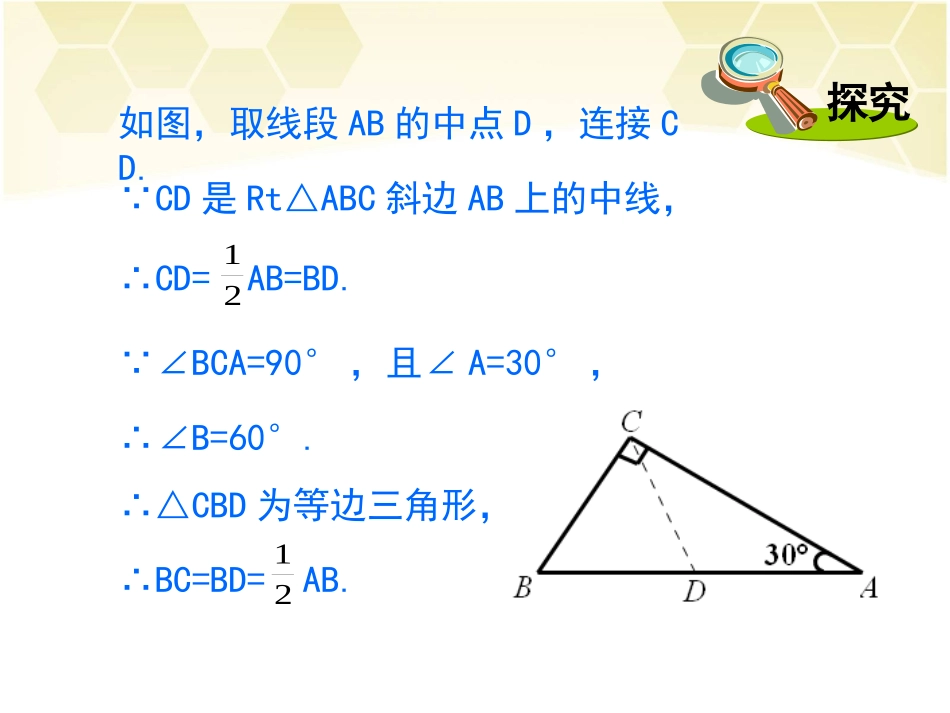
第2课时含30°锐角的直角三角形的性质及其应用1.1直角三角形的性质和判定(Ⅰ)动脑筋如图,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么直角边BC与斜边AB有什么关系呢?∴BC=BD=AB.12如图,取线段AB的中点D,连接CD.∵CD是Rt△ABC斜边AB上的中线,12∴CD=AB=BD.∵∠BCA=90°,且∠A=30°,∴∠B=60°.∴△CBD为等边三角形,探究结论在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.动脑筋如图,在Rt△ABC中,∠BCA=90°,若BC=AB,那么∠A=30°吗?12∴∠A=30°.如图,取线段AB的中点D,连接CD.∵CD是Rt△ABC斜边AB上的中线,12∴CD=AB=BD.∴BC=BD=CD,即△BDC为等边三角形.∴∠B=60°.∵BC=AB,12∵∠A+∠B=90°,探究结论在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.例题例题如图,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距海里.若该船继续保持由西向东的航向,那么有触礁的危险吗?303分析取轮船航向所在的直线为OB.过点A作ADO⊥B,垂足为D.AD长为A岛到轮船航道的最短距离,若AD大于20海里,则轮船由西向东航行就不会有触礁的危险.解如图,过点A作AD⊥OB,垂足为D,连接AO.由于AD长大于20海里,所以轮船由西向东航行不会触礁.于是AD=AO=≈25.98(海里)>20(海里).1303212在Rt△AOD中,AO=海里,∠AOD=30°,303练习1.如图是某商店营业大厅电梯示意图.电梯AB的倾斜角为30°,大厅两层之间的高度BC为6m.你能算出电梯AB的长度吗?解:电梯AB的长度为12m.练习2.如图,在Rt△ABC中,∠ACB=90°,CD垂直于AB,垂足为点D,DB=BC,求∠A的度数.12解:∵CD垂直于AB,DB=BC,∴∠BCD=30°.∴∠B=60°.∵∠ACB=90°,∴∠A=30°.21今天这堂课学了什么内容?反思小结1.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.2.在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.