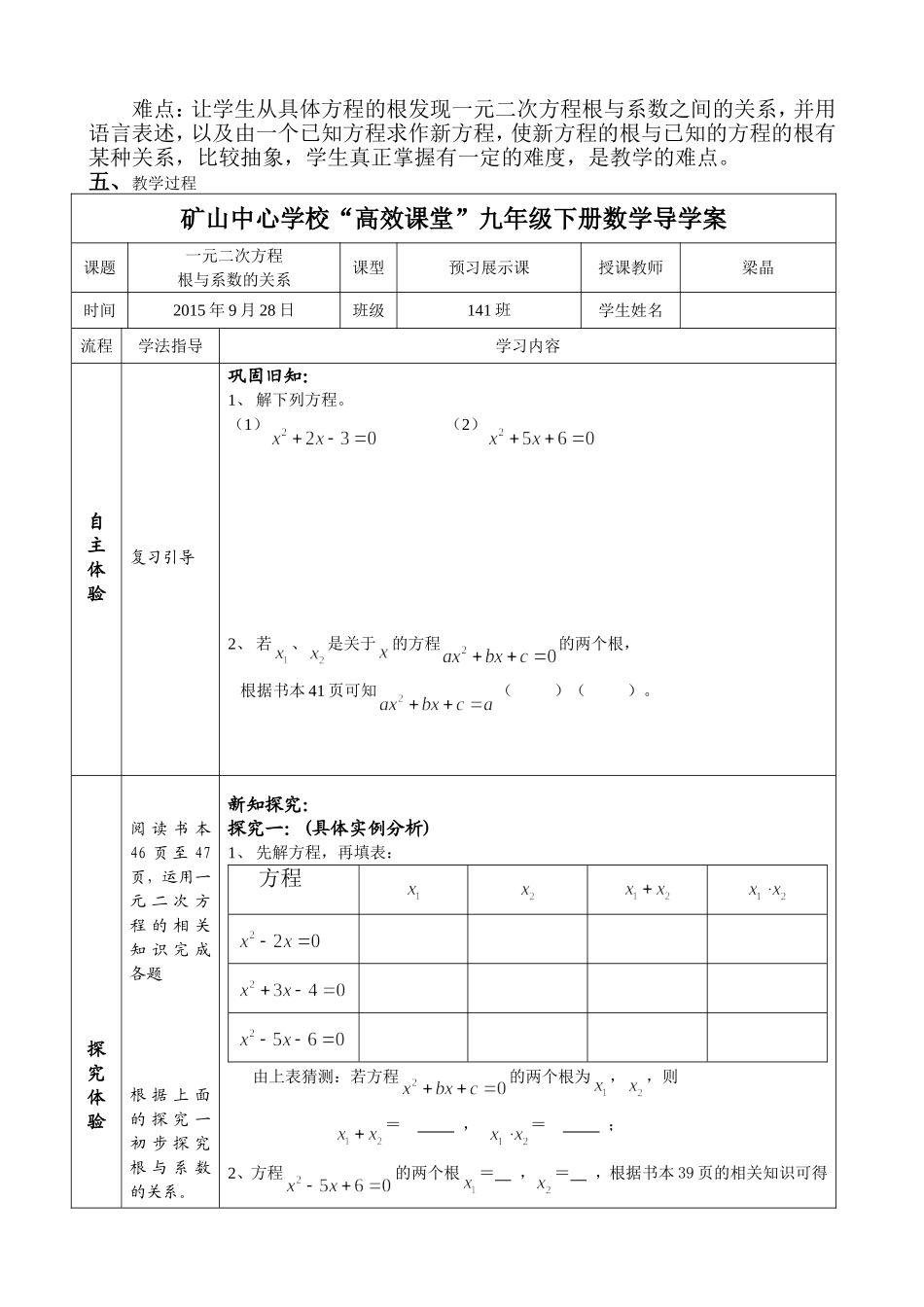
一元二次方程根与系数的关系教学设计矿山中心学校梁晶一、教材分析一元二次方程根与系数的关系(也称韦达定理)是在学习了一元二次方程的解法和根的判别式之后引入的,课标要求通过本节内容的学习能运用韦达定理由已知一元二次方程的一个根求出另一个根与未知数,会求一元二次方程两个根的倒数和、两根的平方和及两根之差;教材通过一元二次方程的根,推导出韦达定理,以及能够建立以数,为根的一元二次方程的方程模型;是对前面知识的巩固与深化,又为以后的知识打下基础,它深化了两根与系数之间的关系,是我们今后继续研究一元二次方程根的情况的主要工具,是方程理论的重要组成部分。韦达定理是初中代数中的一个重要定理,这是因为通过韦达定理的学习,把一元二次方程的研究推向了高级阶段,运用韦达定理可以进一步研究数学中的许多问题,通过近些年的中考数学试卷的分析可以得出:韦达定理及其应用是各地市中考数学命题的热点之一。出现的题型有选择题、填空题和解答题,有的将其与三角函数、几何、二次函数等内容综合起来,形成难度系数较大的压轴题。通过韦达定理的教学,可以培养学生的创新意识、创新精神和综合分析数学问题的能力,也为学生今后学习方程理论打下基础。二、学情分析1、学生已学习用求根公式法解一元二次方程,但是有一部分在把一些较复杂一点的一元二次方程化为一元二次方程的一般形式的时候,要么常在去括号、移项或者合并同类项的时候出问题,要么就在解方程过程中不能正确代入各项系数;或者就在最后不会把计算结果化成最简单的形式;2、本课的教学对象是初中三年级学生,学生对事物的认识多是直观、形象的,他们所注意的多是事物外部的、直接的、具体形象的特征;3、在教学初始,出示一些学生所熟悉和感兴趣的东西,结合一元二次方程求根公式使他们在现代化的教学模式和传统的教学模式相结合的基础上掌握一元二次方程根与系数的关系。三、教学目标知识目标:要求学生在理解的基础上掌握一元二次方程根与系数的关系式,能运用根与系数的关系由已知一元二次方程的一个根求出另一个根与未知数,会求一元二次方程两个根的倒数和与平方数,两根之差。能力目标:通过韦达定理的教学过程,使学生经历观察、实验、猜想、证明等数学活动过程,发展推理能力,能有条理地、清晰地阐述自己的观点,进一步培养学生的创新意识和创新精神。情感目标:通过情境教学过程,激发学生的求知欲望,培养学生积极学习数学的态度。体验数学活动中充满着探索与创造,体验数学活动中的成功感,建立自信心。四、教学重点和难点重点:一元二次方程根与系数的关系。难点:让学生从具体方程的根发现一元二次方程根与系数之间的关系,并用语言表述,以及由一个已知方程求作新方程,使新方程的根与已知的方程的根有某种关系,比较抽象,学生真正掌握有一定的难度,是教学的难点。五、教学过程矿山中心学校“高效课堂”九年级下册数学导学案课题一元二次方程根与系数的关系课型预习展示课授课教师梁晶时间2015年9月28日班级141班学生姓名流程学法指导学习内容自主体验复习引导巩固旧知:1、解下列方程。(1)(2)2、若、是关于的方程的两个根,根据书本41页可知()()。探究体验阅读书本46页至47页,运用一元二次方程的相关知识完成各题根据上面的探究一初步探究根与系数的关系。新知探究:探究一:(具体实例分析)1、先解方程,再填表:方程由上表猜测:若方程的两个根为,,则=,=;2、方程的两个根=,=,根据书本39页的相关知识可得运用一元二次方程的有关知识得出根与系数的关系(韦达定理)。(—)(—)。探究二:(韦达定理的推导)对于方程,当△≥0时,该方程的根与它的系数之间有什么关系呢?当△≥0时,设的两个根为、,则(—)(—)=()+,又于是=,由上式可得根与系数的关系式:即,根据探究一、探究二得出韦达定理:当△≥0时,一元二次方程的根与系数之间的关系:两根的和等于,即:两根的积等于,即:合作展示体验25先自己完成再分小组讨论,形成小组共识。活动一口头展示,抢答活动二小组选派人到黑板上展示,并说活动一:(根与系数的关系)例:若、是方程...