指数与指数函数复习VIP免费

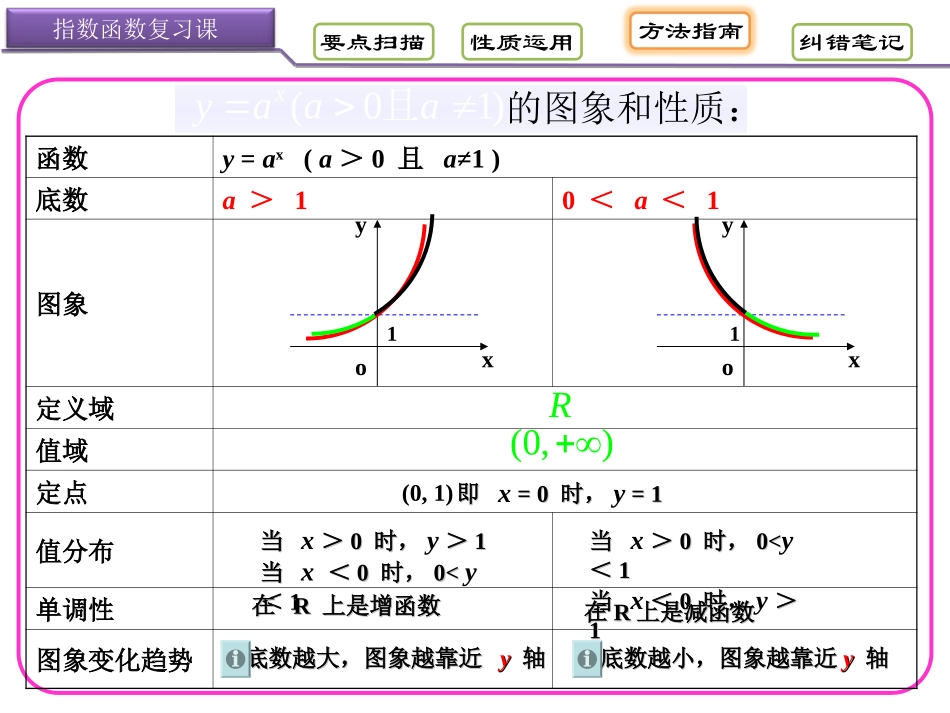
基本初等函数(Ⅰ)复习课纠错笔记方法指南要点扫描2(3,4)指数函数复习课[2,+∞)a>1[1,+∞)性质运用热身训练热身训练热身训练热身训练._________,)12()(.4________3.3_______________,3.2_____)21()10(.132aaxfayya，yyaaayxxxxx范围是的取值则实数是R上的增函数函数恒过定点函数值域是的定义域是则轴对称的图象关于的图象与函数且若函数纠错笔记要点扫描方法指南指数函数复习课的图象和性质：(01)xyaaa且函数y=ax(a＞0且a≠1)底数a＞10＜a＜1图象定义域值域定点值分布单调性图象变化趋势(0,)R(0,1)即即x=0=0时，时，y=1=1当当x＞＞00时，时，y＞＞11当当x＜＜00时，时，0<02，则函数y=ax和y=(a－1)x2在同坐标系中的图象只能是图中的()ABA拓展练习拓展练习纠错笔记要点扫描方法指南.1.cdbaDdcbaA1.cdabB1.dcbaC1.(1)(2)(3)(4)OXy指数函数复习课4.(1),(2),(3),(4),,,,1.xxxxyaybycydabcd如图是指数函数的图象则与的大小关系是（）B性质运用纠错笔记要点扫描方法指南性质运用利用指数函数比较大小利用指数函数比较大小题型1题型1指数函数复习课<<>比较大小的方法①构造函数的方法:数的特征是同底不同指(包括可转化为同底的)②搭桥比较法:用特殊的数1.20.2530.6410.330.76(1)(3)_____(3);33(2)()_____();4445(3)()______();54(4)6______0.7.>指数函数复习课纠错笔记要点扫描方法指南利用函数单调性求解指数函数不等式利用函数单调性求解指数函数不等式题型2题型2性质运用2213.2(2)_______.xxaaaax已知（），则的取值范围是31212121.2,2,,.xxyyxyy设当为何值时27412.(01)xxaaaa求不等式且的解集.要点扫描方法指南性质运用忽视对底数的讨论致错忽视对底数的讨论致错易错点1易错点1101.xyaaa例1求函数，且的定义域解解解解正解正解正解正解1010,xxaax，，由得解得1).0,,10xyaaa函数且的定义域为［故110,01,);xayaaa时，函数且的定义［域为当0110,(,01.xayaaa时，函数且的定义域为］当指数函数复习课错解错解错解错解1.xaa对底数进行分解不等式时需类讨论纠错笔记纠错笔记纠错指津要点扫描方法指南纠错笔记忽视指数函数值域致错忽视指数函数值域致错易错点2易错点2142xy例2求函数的值域。解解解解正解正解正解正解1410214xx因为所以，，14|R12xyyyy函数的值域，且为故。010,xyaaa指数函数，且的值域为由于，14|012xyyyy函数的值域，且为故。纠错指津指数函数复习课错解错解错解错解，在指数解答函数的值指数函数域为全体正数时应留意。性质运用纠错笔记纠错笔记要点扫描方法指南简单的复合函数简单的复合函数题型3题型3指数函数复习课性质运用3.421xxy求函数的值域。11.2____()xyR函数在上为填增或减函数。2212.()_______3xxy函数的单调增区间是。减(-∞,1]若x[-3,2]∈呢？换元思想很重要！同增异减基本初等函数(Ⅰ)复习课总结一下本节课你的收获是什么？纠错笔记要点扫描方法指南指数函数复习课性质运用1.指数函数的图象2.指数函数图象和性质的运用3.数学思想:数形结合、分类讨论4.方法指南:解决有关大小、不等式、简单的复合函数等问题首先要看底数的取值,灵活应用指数函数的性质.课堂小结课堂小结xyo1xyo1a＞10＜a＜1•课外同步训练