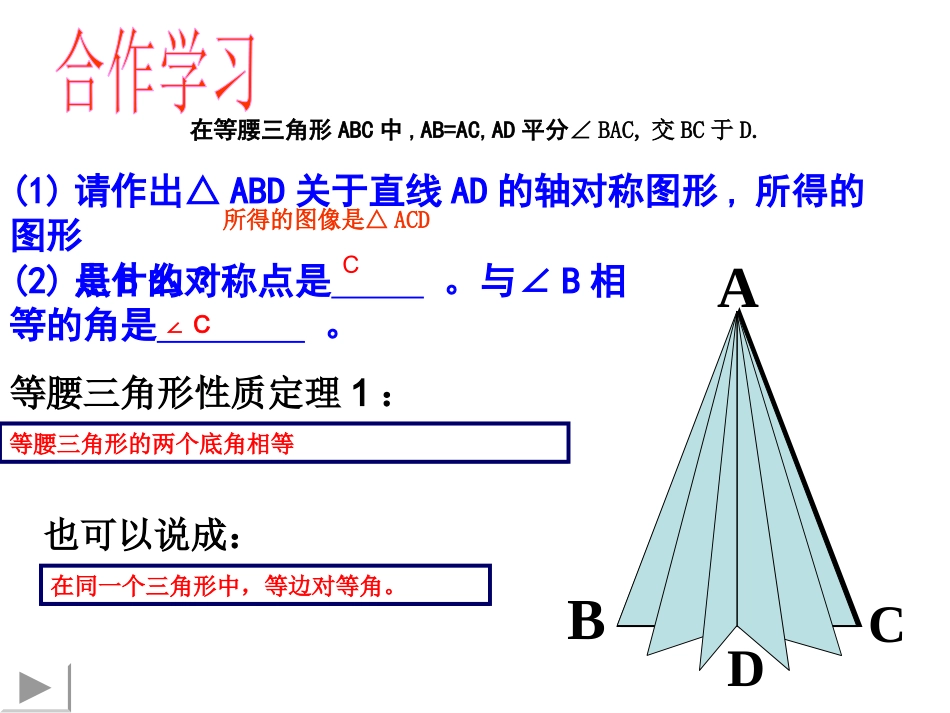
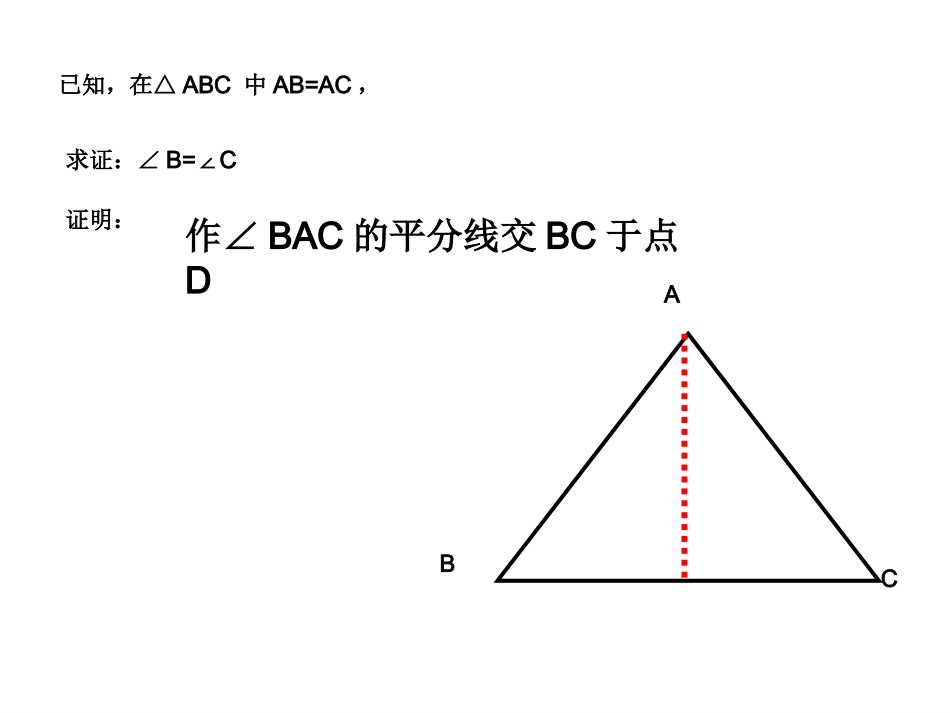
2.3等腰三角形的性质定理(1)在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.(1)请作出△ABD关于直线AD的轴对称图形,所得的图形是什么?DABC(2)点B的对称点是。与∠B相等的角是。所得的图像是△ACD∠CC等腰三角形性质定理1:等腰三角形的两个底角相等也可以说成:在同一个三角形中,等边对等角。ACBD已知,在△ABC中AB=AC,求证:∠B=C∠证明:作∠BAC的平分线交BC于点D例1:求等边三角形ABC的三个内角的度数。ACB推论:等边三角形的各个角都等于60°。例2.求证等腰三角形两底角的平分线相等。ACBED已知:如图在△ABC中,AB=AC,BD、CE是△ABC的两条角平分线。求证:BD=CE证明:练习、已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。ABC变式练习1:已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。ABCBA变式练习2:已知:等腰三角形的一个内角为80°,求另两个角的度数.100°知道何时要分类了吗?判断下列语句是否正确。(1)有一个角是60°的等腰三角形,其它两个内角也为60°.()(2)等腰三角形的底角都是锐角.()(3)钝角三角形不可能是等腰三角形.()(4)等腰三角形的顶角一定是锐角。()×作业×1.等腰三角形一个底角为75°,它的另外两个角为_______⒉等腰三角形一个角为70°,它的另外两个角为__________________⒊等腰三角形一个角为110°,它的另外两个角为______试一试试一试75°,30°75°,30°70°,40°或55°,55°35°,35°1.已知:如图,在△ABC中AB=AC,P为BC的中点,D、E分别为AB、AC上的点,且AD=AE。ABCPDE求证:PD=PE2.如图,AB=AC,若D是上BC任意一点,DEAB⊥,DFAC⊥,CHAB⊥,垂足分别E,F,H,FABCDEH求证:DE+DF=CH利用“面积法”