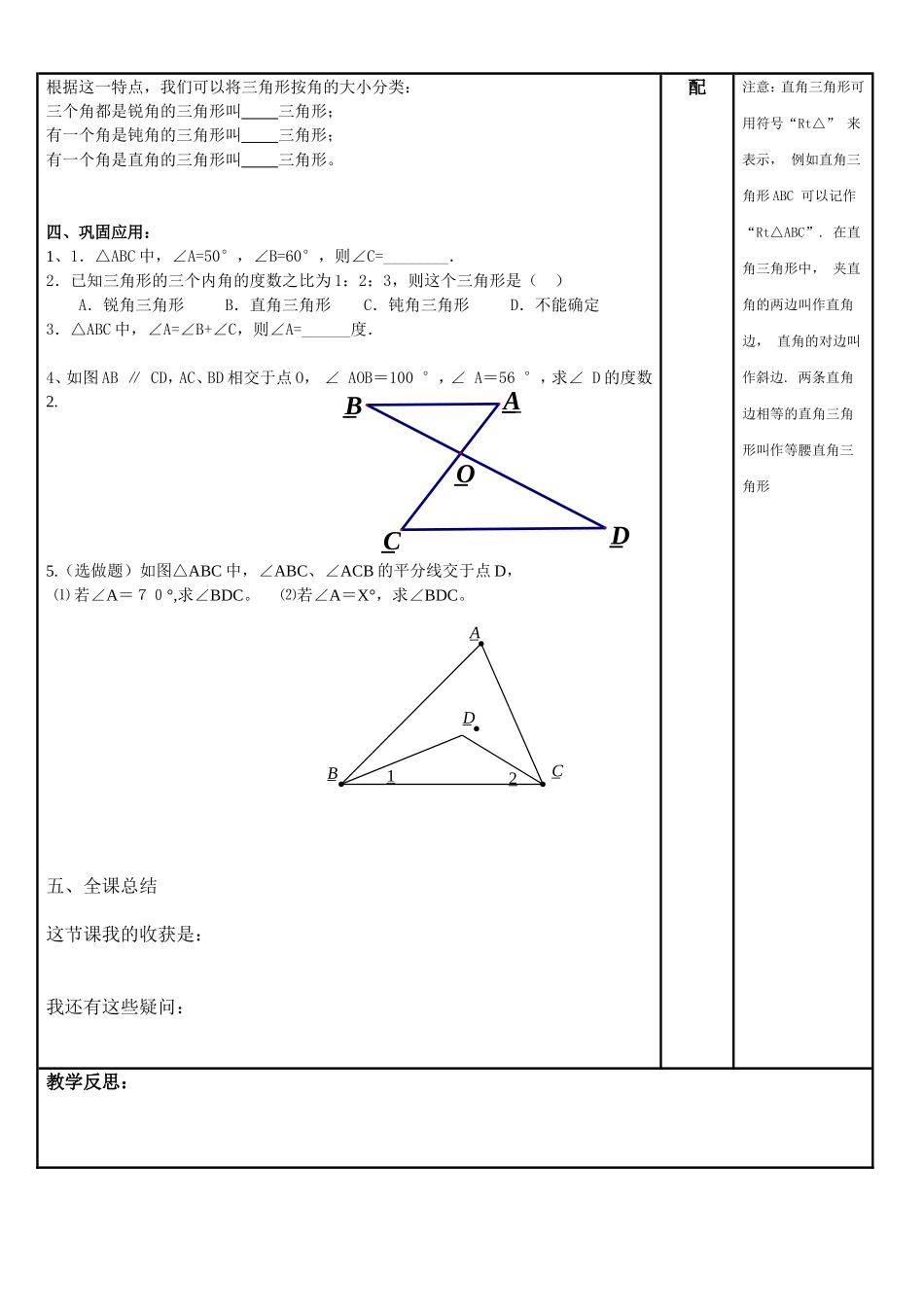
禾青中心学校导学案科目:_数学年级:_八主备人:喻四梅审核人:_____时间:10.12课题三角形的内角和共课时第课时学习目标1、知道三角形内角和的性质及三角形的分类。2、能理解和掌握三角形内角和定理的证明过程,感受辅助线在证明中的魅力。3、能灵活应用三角形内角和定理进行简单的计算和推理证明。重点难点重点:三角形内角和的性质及三角形的分类难点:灵活应用三角形内角和定理进行简单的计算和推理证明学习内容时间分配学习方法一、知识链接如图,直线a、b被直线c所截,且a∥b,则:∠1____∠4(两直线平行,。)∠3____∠4(两直线平行,。)∠2___∠4=____(两直线平行,。二、预习交流认真阅读P46内容。完成以下问题:⑴将△ABC的边BC所在的直线平移至点A可以得到。,⑵根据平行线的性质,这样就可以将∠B转移到将∠C转移到⑶这样就将三角形的三个内角和转移到一起构成了一个。(说明:为了证明的需要,在原来的图形上添画的线叫作辅助线。在平面几何里,辅助线通常画成虚线。)二、合作探究(一)三角形的内角和定理如图:已知点D在△ABC中BC的延长线上,CE∥AB,你能根据这些条件,说明∠A+∠B+∠ACB=180°吗?通过以上证明:我们可以得到三角形的内角和定理:(二)、三角形的分类思考、讨论:一个三角形的三个内角中,最多有几个直角?最多有几个钝角?提示:根据平行线的性质,我们常常通过构建平行线将已知角转移到其它的位置。小组长组织讨论完成左边的根据三角形的内角和定理思考。组内讨论学习内容时间分学习方法_4_3_2_1_b_a_c21ABC21ABCED配根据这一特点,我们可以将三角形按角的大小分类:三个角都是锐角的三角形叫三角形;有一个角是钝角的三角形叫三角形;有一个角是直角的三角形叫三角形。四、巩固应用:1、1.△ABC中,∠A=50°,∠B=60°,则∠C=________.2.已知三角形的三个内角的度数之比为1:2:3,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定3.△ABC中,∠A=∠B+∠C,则∠A=______度.4、如图AB∥CD,AC、BD相交于点O,∠AOB=100°,∠A=56°,求∠D的度数2.5.(选做题)如图△ABC中,∠ABC、∠ACB的平分线交于点D,⑴若∠A=70°,求∠BDC。⑵若∠A=X°,求∠BDC。五、全课总结这节课我的收获是:我还有这些疑问:注意:直角三角形可用符号“Rt△”来表示,例如直角三角形ABC可以记作“Rt△ABC”.在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边.两条直角边相等的直角三角形叫作等腰直角三角形教学反思:_A_D_C_O_B_2_1_A_B_C_D