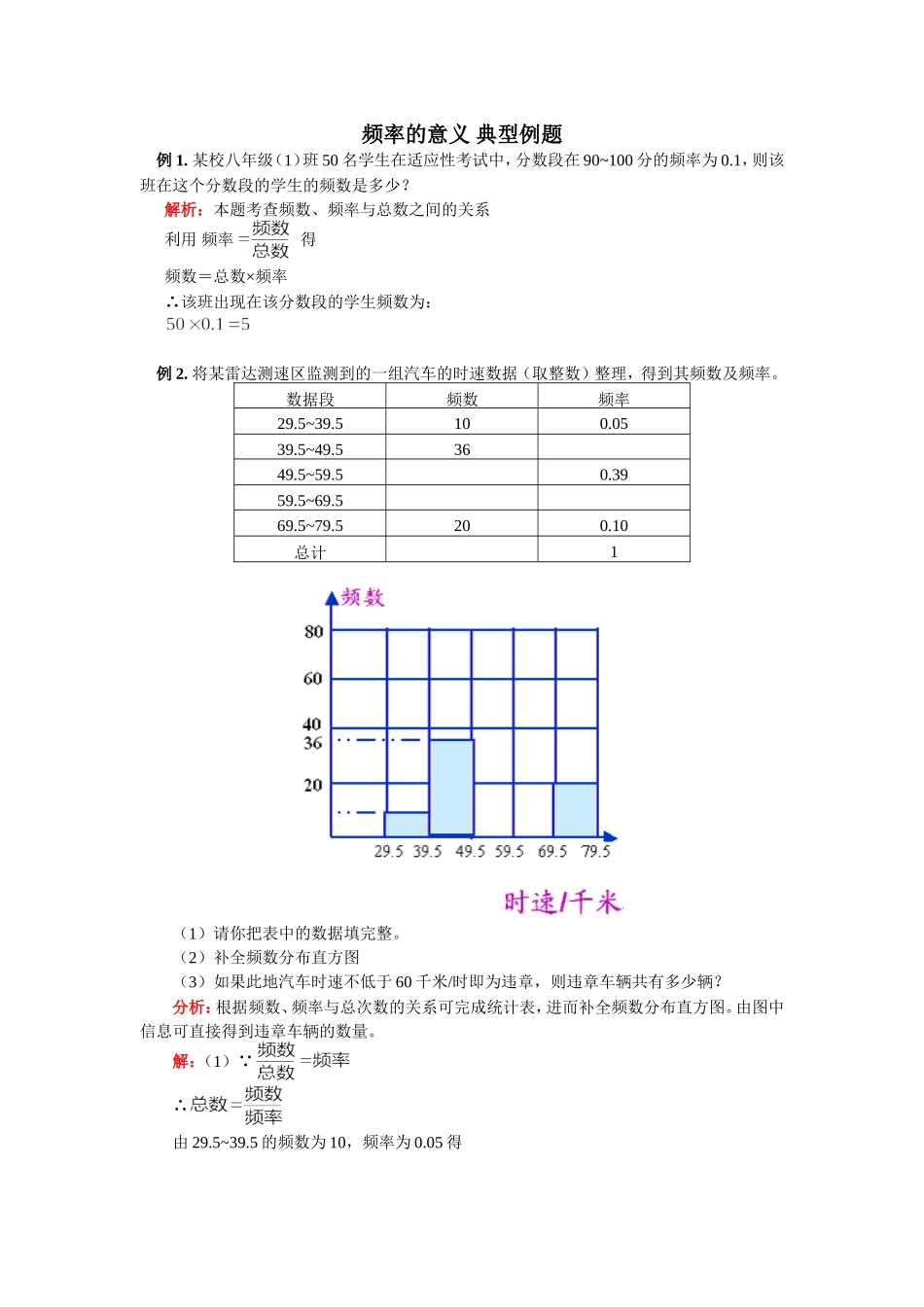
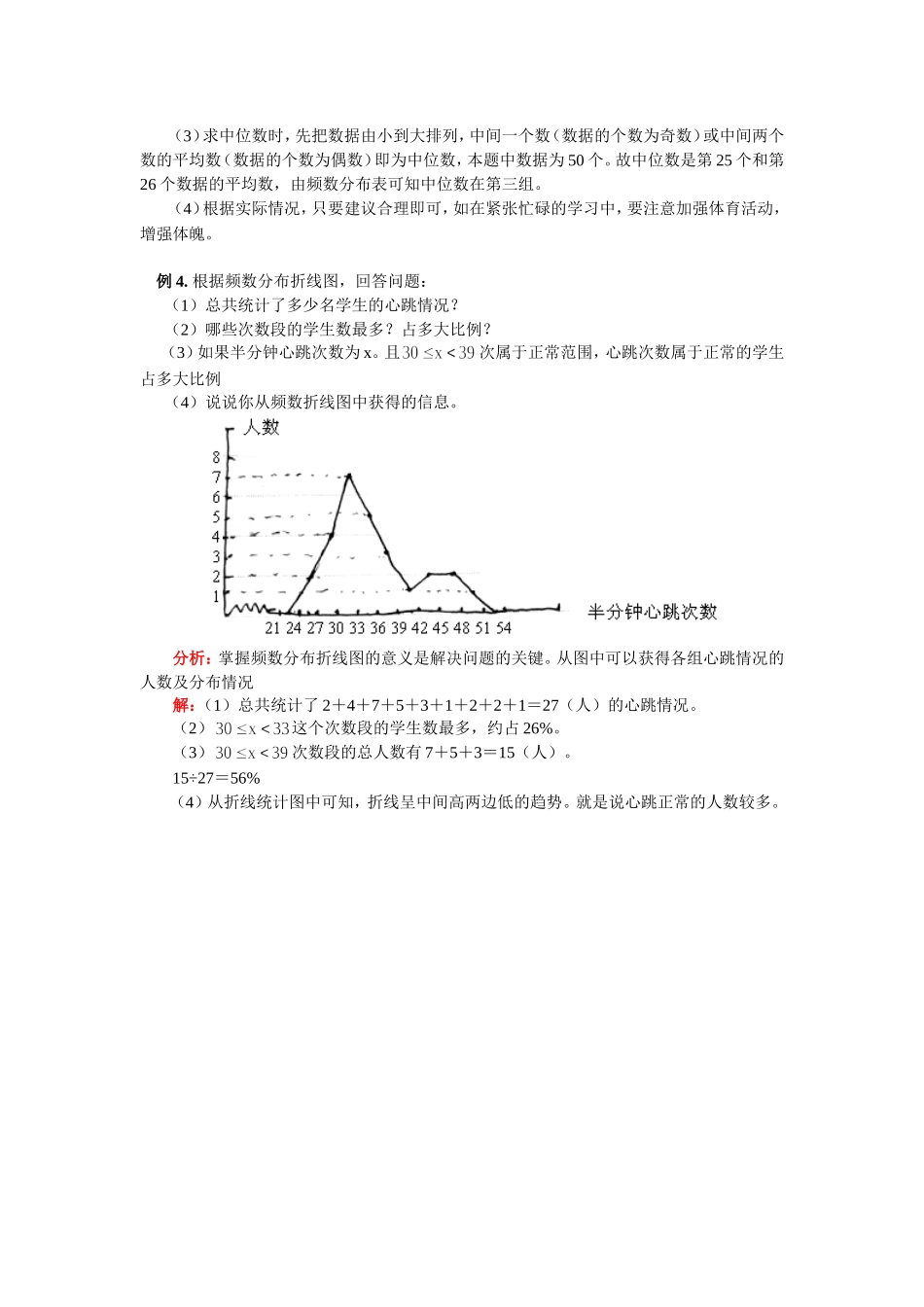
频率的意义典型例题例1.某校八年级(1)班50名学生在适应性考试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生的频数是多少?解析:本题考查频数、频率与总数之间的关系利用频率得频数=总数×频率∴该班出现在该分数段的学生频数为:例2.将某雷达测速区监测到的一组汽车的时速数据(取整数)整理,得到其频数及频率。数据段频数频率29.5~39.5100.0539.5~49.53649.5~59.50.3959.5~69.569.5~79.5200.10总计1(1)请你把表中的数据填完整。(2)补全频数分布直方图(3)如果此地汽车时速不低于60千米/时即为违章,则违章车辆共有多少辆?分析:根据频数、频率与总次数的关系可完成统计表,进而补全频数分布直方图。由图中信息可直接得到违章车辆的数量。解:(1)∵∴由29.5~39.5的频数为10,频率为0.05得总数∴39.5~49.5的频率为:49.5~59.5的频数为:200×0.39=7859.5~69.5的频数为:200-(10-36-78-20)=56频率为总计,200(2)根据(1)中补全的数据,补全频数分布直方图(3)由频数分布表或频数分布直方图可知。时速超过60千米的有辆汽车。例3.为了进一步了解八年级学生的身体素质情况,体育老师对八(1)班50名学生进行了一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图组别次数频数一二三四五请结合图表完成下列问题:(1)表中的;(2)请把频数分布直方图补充完整;(3)这个样本数据的中位数落在第组;(4)若八年级学生一分钟跳绳次数的达标要求是:不合格;为合格;为良;为优.根据以上信息,请你给学校或八年级同学提一条合理化建议:.分析:综合题目及频数分布表可得a的值,从而可补全频数分布直方图。解:(1)各小组频数之和为50,故可求得a=12(2)由频数分布表可把直方图补充完整。(3)求中位数时,先把数据由小到大排列,中间一个数(数据的个数为奇数)或中间两个数的平均数(数据的个数为偶数)即为中位数,本题中数据为50个。故中位数是第25个和第26个数据的平均数,由频数分布表可知中位数在第三组。(4)根据实际情况,只要建议合理即可,如在紧张忙碌的学习中,要注意加强体育活动,增强体魄。例4.根据频数分布折线图,回答问题:(1)总共统计了多少名学生的心跳情况?(2)哪些次数段的学生数最多?占多大比例?(3)如果半分钟心跳次数为x。且次属于正常范围,心跳次数属于正常的学生占多大比例(4)说说你从频数折线图中获得的信息。分析:掌握频数分布折线图的意义是解决问题的关键。从图中可以获得各组心跳情况的人数及分布情况解:(1)总共统计了2+4+7+5+3+1+2+2+1=27(人)的心跳情况。(2)这个次数段的学生数最多,约占26%。(3)次数段的总人数有7+5+3=15(人)。15÷27=56%(4)从折线统计图中可知,折线呈中间高两边低的趋势。就是说心跳正常的人数较多。