期末复习六　直线与圆的位置关系VIP免费

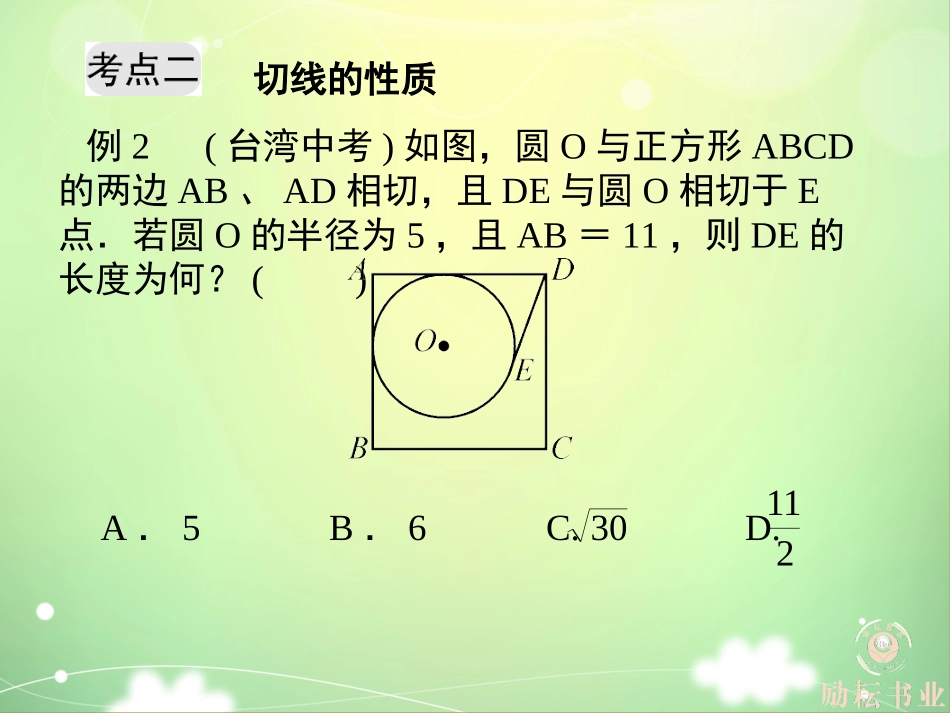
期末复习六直线与圆的位置关系直线与圆的位置关系的判定例1(张家界中考)如图，∠O＝30°，C为OB上一点，且OC＝6，以点C为圆心，半径为3的圆与OA的位置关系是()A．相离B．相交C．相切D．以上三种情况均有可能答案：过点C作CDAO⊥于点D，∵∠O＝30°，OC＝6，∴DC＝3，∴以点C为圆心，半径为3的圆与OA的位置关系是：相切．故选：C.反思：判断直线与圆的位置关系，常根据圆心到直线的距离d与圆的半径r的大小确定：(1)若d＜r，则直线与圆相交；(2)若d＝r，则直线与圆相切；(3)若d＞r，则直线与圆相离．切线的性质例2(台湾中考)如图，圆O与正方形ABCD的两边AB、AD相切，且DE与圆O相切于E点．若圆O的半径为5，且AB＝11，则DE的长度为何？()A．5B．6C.D.30211答案：连结OM、ON，∵四边形ABCD是正方形，∴AD＝AB＝11，∠A＝90°，∵圆O与正方形ABCD的两边AB、AD相切，∴∠OMA＝∠ONA＝90°＝∠A，∵OM＝ON，∴四边形ANOM是正方形，∴AM＝OM，∵AD和DE与圆O相切，圆O的半径为5，∴AM＝5，DM＝DE，∴DE＝11－5＝6，故选B.反思：解题关键是求出AM长和得出DE＝DM.切线的判定与性质例3(毕节中考)如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连结AD交BC于F，AC＝FC.(1)求证：AC是⊙O的切线；(2)已知圆的半径r＝5，EF＝3，求DF的长．答案：(1)证明：连结OA，OD，∵D为BE的下半圆弧的中点，∴ODBE⊥，∴∠D＋∠DFO＝90°，∵AC＝FC，∴∠CAF＝∠CFA，∵∠CFA＝∠DFO，∴∠CAF＝∠DFO，而OA＝OD，∴∠OAD＝∠ODF，∴∠OAD＋∠CAF＝90°，即∠OAC＝90°，∴OAAC⊥，∴AC是⊙O的切线；(2)∵圆的半径r＝5，EF＝3，∴OF＝2，在RtODF△中，∵OD＝5，OF＝2，∴DF＝.29反思：证明某直线为圆的切线时，如果已知直线与圆有公共点，即可作出过该点的半径，证明直线垂直于该半径，即“作半径，证垂直”；如果不能确定某直线与已知圆有公共点，则过圆心作直线的垂线段，证明它到圆心的距离等于半径，即“作垂直，证半径”．在证明垂直时，常用到直径所对的圆周角是直角．切线长定理的运用例4(1)(宜宾中考)如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝40°，则∠BAC＝________．(2)(烟台中考)如图，直线ly∶＝－x＋1与坐标轴交于A，B两点，点M(m，0)是x轴上一动点，以点M为圆心，2个单位长度为半径作⊙M，当⊙M与直线l相切时，则m的值为________．21如图，设⊙M与AB相切于C，连结MC，则MC＝2，MCAB⊥，∵∠MCB＝∠AOB＝90°，∠B＝∠B，∴△BMCBAO∽△，∴即∴BM＝2，∴OM＝2－2，同理可得OM′＝2＋2.∴m＝2－2或m＝2＋2.故答案为：2－2，2＋2.答案：(1)20°(2)在y＝－x＋1中，令x＝0，则y＝1，令y＝0，则x＝2，∴A(0，1)，B(2，0)，∴AB＝；215,ABBMOACM,512BM5555555反思：(1)根据切线的性质和切线长定理进行计算求出角的度数；(2)注意分类讨论是解题的关键，求直线与圆的位置关系时，在图形不明确的情况下，要分类讨论，不要漏解．三角形的内切圆例5(1)如图，O是△ABC的内心，过点O作EF//AB，与AC、BC分别交于E、F，则()A．EF＞AE＋BFB．EF＜AE＋BFC．EF＝AE＋BFD．EF≤AE＋BF(2)如图，⊙O是△ABC的内切圆，切点分别是D、E、F，已知∠A＝100°，∠C＝30°，则∠DFE的度数是()A．55°B．60°C．65°D．70°反思：(1)作出辅助线，构造出等腰三角形是解答此题的关键；(2)运用三角形的内角和定理、四边形的内角和定理以及切线的性质定理、圆周角定理．三角形的外接圆与三角形的内切圆，注意弄清“内”与“外”，“接”与“切”的含义．答案：(1)C(2)C圆的综合性问题例6(临沂中考)如图，点O为RtABC△斜边AB上一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连结AD.(1)求证：AD平分∠BAC；(2)若∠BAC＝60°，OA＝2，求阴影部分的面积(结果保留π)．答案：(1)∵⊙O切BC于D，∴ODBC⊥，∵ACBC⊥，∴AC//OD，∴∠CAD＝∠ADO，∵OA＝OD，∴∠OAD＝∠ADO，∴∠OAD＝∠CAD，即AD平分∠CAB；(2)设EO与AD交于点M，连结ED.∵∠BAC＝60°，OA＝OE，∴△AEO是等边三角形，∴AE＝OA，∠AOE＝60°，∴AE＝AO＝OD，又由(1)知，AC//OD即AE//OD，∴四边形AEDO是菱形，则△AEM≌DOM△，∠EOD＝60°，∴SAEM△＝SDMO△，∴S阴影＝S扇形EOD＝＝.323602602反思：注意掌握辅助线的作法，注意数形结合思想的应用．