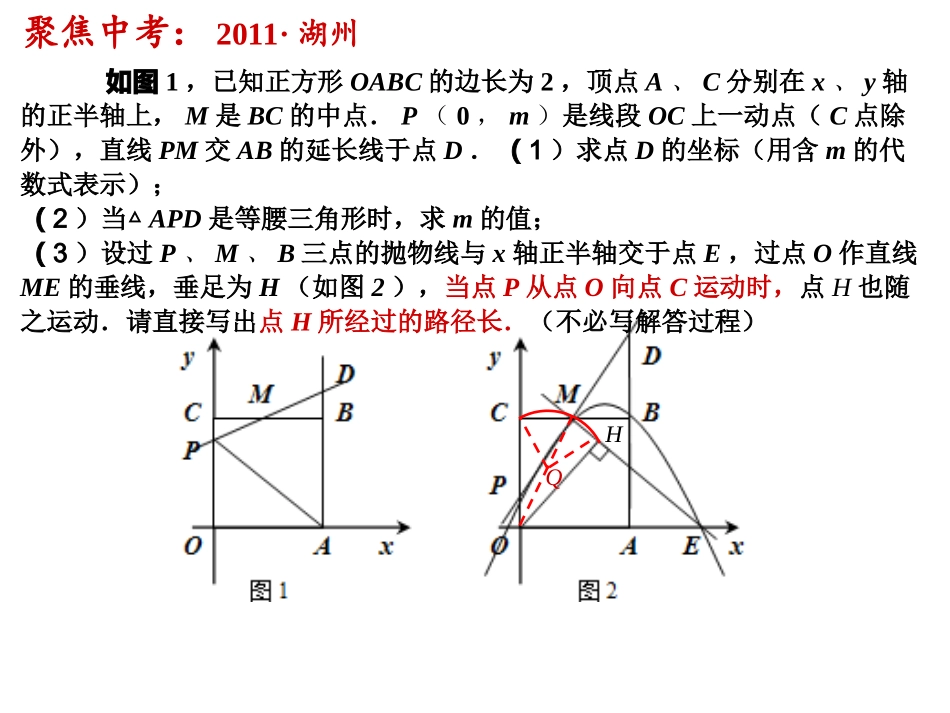
专题复习:动点的路径长问题等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.(1)若AE=CF,①求证:AF=BE,并求∠APB的度数;②若AE=2,试求AP·AF的值;(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.聚焦中考:2014·金华AEPFCB聚焦中考:2011·湖州如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.(1)求点D的坐标(用含m的代数式表示);(2)当△APD是等腰三角形时,求m的值;(3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2),当点P从点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)QH如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.(1)当点P运动到线段OA的中点时,点C的坐标为_________;(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.聚焦中考:2012·义乌聚焦中考:2013·十堰如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)如图2,抛物线顶点为E,EF⊥x轴于F点,一动点M从点E出发,沿线段EF匀速运动到点F,过点M作CM的垂线交x轴于点N,求点N经过的路径长..课本原题:八年级上册第二章《特殊三角形》第87页28题如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿着墙面下滑0.4米,那么点B运动的路径长为多少米?如图,一架2米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为1米,如果梯子的顶端A沿着墙面下滑到点C处停止,那么梯子AB的中点P所经过的路径长为多少米?变式:ACBPP′例:如图,正方形ABCD的边长为4,点E、F分别是边BC、BA上的动点,且满足BE=BF,连接AE、CF相交于点P.当点E由点B运动到点C时,求点P经过的路径长.ABCDEFPOACDEFP变式一:如图,正方形ABCD的边长为4,点E、F分别是边BC、CD上的动点,且满足BE=CF,连接AE、BF相交于点P.当点E由点B运动到点C时,求点P经过的路径长.BOP′变式二:已知正方形ABCD的边长为4,点E是边BC上的动点,点F在正方形边上运动,且满足AE=BF,AE、BF相交于点P.当点E由点B运动到点C时,求点P经过的路径长.聚焦中考:2013·十堰如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)如图2,抛物线顶点为E,EF⊥x轴于F点,一动点M从点E出发,沿线段EF匀速运动到点F,过点M作CM的垂线交x轴于点N,求点N经过的路径长..