对数与对数运算第课时对数的运算VIP免费

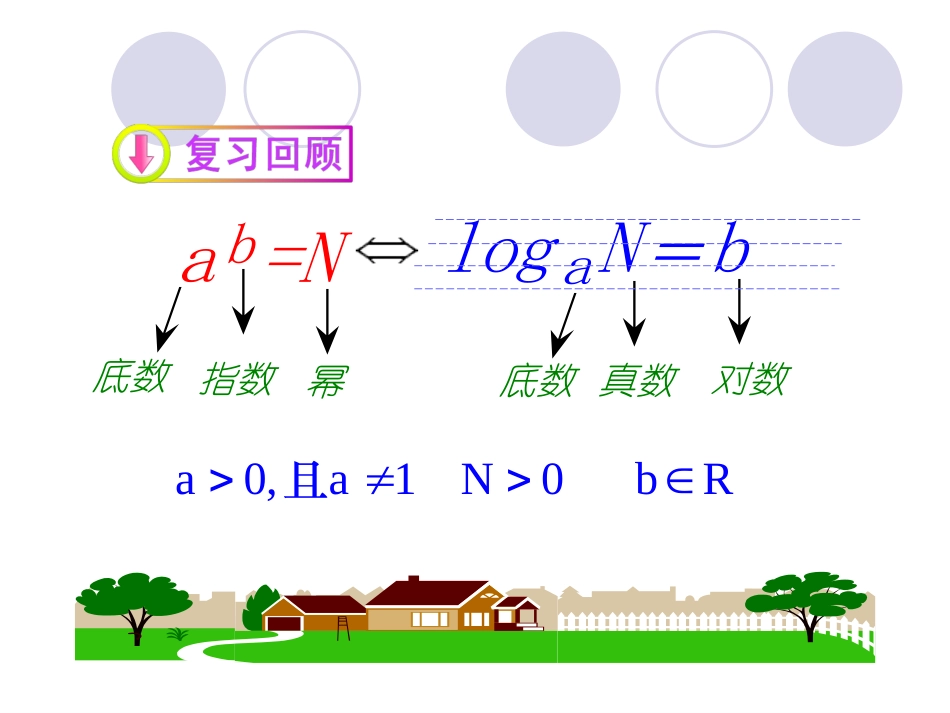
第2课时对数的运算1.理解对数的运算性质；（重点）2.知道用换底公式能将一般对数转化成自然对数或常用对数；（难点）3.通过阅读材料，了解对数的发展史以及对简化运算的作用．底数对数真数幂指数底数↓↓↓↓↓↓logaN＝bab=Na0,a1N0bR且性质：log1.aNaN3.log10a4.log1aa２.负数和零没有对数(,)(,)()(,)()()mnmnmmnnmnmnnnnaaamnRaamnRaaamnRababnR指数运算法则：logaMlogaN=?+,pqMaNa1.对数的运算性质pqpqMNaaa探究一：化为对数式，结合指数的运算性质能否将化为对数式？将指数式它们之间有何关系？试一试:由,pqMaNa得log,logaapMqN由pqpqMNaaa得log()apqMN从而得出log()loglogaaaMNMN(0,1,0,0)且aaMN探究二：结合前面的推导，由指数式ppqqMaaNa又能得到什么样的结论？试一试:由ppqqMaaNa得logloglogaaaMpqMNN(0,1,0,0)且aaMN()npnnpMaa又能得到什么样的结论？试一试:由()npnnpMaa得loglognaaMnpnM(a0,a1,M0,nR)且探究三：结合前面的推导，由指数式log()loglogaaaMNMNlogloglogaaaMMNNloglognaaMnM0,0,)MNnR结论：对数的运算性质(a>0,且a≠1;22332logloglogaaaxyxyzz112logloglog23aaaxyz23logloglogaaaxyz1loglogloglogloglog:aaaaaaxyxyzxyzz解用表示下列各式:lg,lg,lgxyz232(1)lg();(2)lg;(3)lg;(4)lg.xyxyzzxyxyzz(1)lg()lglg()xyzxyz解：22(2)lglg()lgxyxyzz33(3)lglg()lgxyxyzz2(4)lgxyzlglglgxyzlg2lglgxyz1lg3lglg2xyz2lglg()xyz1lg2lglg2xyz点评：牢记对数的运算法则，直接利用公式.例2求下列各式的值：（1）（2）752log(42)5lg100（2）5lg10025lg1025解：(1)752log(42)72log452log227log425log2725119（1）7lg142lglg7lg183例3计算：（2）lg243lg9lg27lg83lg10lg1.2解：（1）方法一：72lg3lg2lg72(lg7lg3)lg7(lg22lg3)0lg(27)2lg(23)（3）公式的直接应用方法二：27lg14lg()lg7lg1832147lg7()183lg107lg142lglg7lg183公式的逆用5lg32lg3521133222lg27lg83lg10(3)lg1.2lg(3)lg23lg(10)32lg1052lg243lg3(2)lg9lg33(lg32lg21)2lg32lg2132点评：注意公式的正用，逆用.对于底数相同的对数式的化简,常用的方法是:(1)“收”:将同底的两对数的和(差)收成积(商)的对数.(2)“拆”:将积(商)的对数拆成对数的和(差).(3)对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.提升总结：（1）（4）（3）（2）1.求下列各式的值：33log5log15lg5lg2551log3log322log6log3226loglog213lg(52)lg101551log(3)log1031335loglog31152321lgx,lgy,lgzx1lg(xyz);2lgyz.用表示下列各式；（）（）2321lg(xyz)lgx2lgy3lgzx1(2)lglgxlgy2lgzyz:2案（）答2223log32loglog64答案：82.（2012·威海高一检测）计算3331lg2lg5;(2)log45log5.不用计算器，求下列各式的值；（）(1)lg2lg5lg(25)解：lg1012lg101lg1021233345(2)log45log5log53log923log332log321.对数的运算法则；2.利用定义及指数运算证明对数的运算法则；3.对数运算法则的应用；4.换底公式的证明及应用.积、商、幂的对数运算法则：如果a>0，且a1，M>0，N>0,那么：log()loglogaaaMNMNlogloglogaaaMMNNloglog)naaMnMnR（探究四：结合对数的定义，你能推导出对数的换底公式吗?logloglogcacNNa(a>0,且a≠1;c>0,且c≠1;N>0)证明：设由对数的定义可得：,pNa即证得logaNploglogpccNaloglog,ccNpaloglogccNpalogloglogcacNNa这个公式叫做换底公式用换底公式证明：1loglogabbaloglognmaambbn23454839(1)loglog(2)log3log4log5log2(3)(log3log3)(log2log2)acca(1)loglogacca解:lglg1;lglgcaac2345(2)log3log4log5log2lg3lg4lg5lg21;lg2lg3lg4lg51.利用对数的换底公式化简下列各式4839(3)(log3log3)(log2log2)232lg3lg3lg2lg2()()lg2lg2lg3lg3lg3lg3lg2lg2()()2lg23lg2lg32lg35lg33lg25.6lg22lg34lg3lg3lg2lg2()()lg4lg8lg3lg923456741log3log4log5log6log7log8,2loglog;baab.（2012潍坊高一检测）利用换底公式，计算下列各式的值；（）（）234567(1)log3log4log5log6log7log8解：lg3lg4lg5lg6lg7lg8lg2lg3lg4lg5lg6lg7lg8lg23lg2lg23lg2lg23lglg(2)logloglglgbaababba1不渴望能够一跃千里，只希望每天能够前进一步。