岳云中学2017年下学期高二期中考试VIP免费

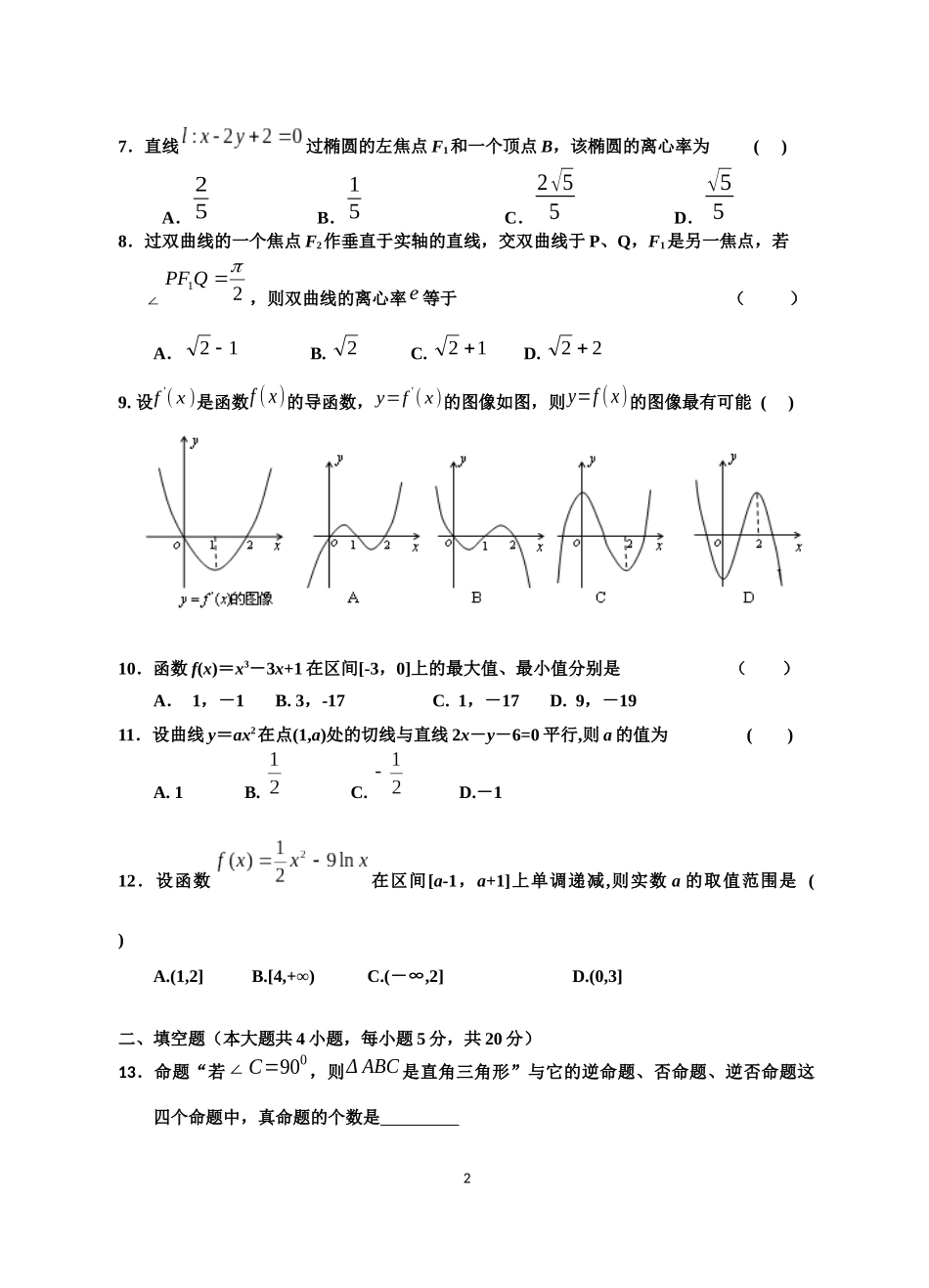
岳云中学2017年下学期高二期中考试数学（文科）试题班级姓名学号一、选择题(本大题共12小题,每小题5分,共60分)1．“”是“”的()A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件2．已知命题p:“|x－2|≥2”,命题“q:x∈Z”,如果“p且q”与“非q”同时为假命题,则满足条件的x为（）A.{x|x≥3或x≤－1,x∉Z}B.{x|－1≤x≤3,x∉Z}C.{－1,0,1,2,3}D.{1,2,3}3．有以下四个命题：①若，则.②若lgx有意义,则.③若,则.④若,则.则是真命题的序号为()A．①②B．①③C．②③D．③④4．命题“”的否定是()A．不存在B．存在C．存在D．对任意的5．双曲线的焦距为()A．B．C．D．6．某校为了研究学生性别和对待某一活动的态度(支持与不支持)的关系，运用2×2列联表进行独立性检验，经计算K2＝7.069，则有多大把握认为“学生性别与支持该活动有关系”．21A．0.1%B．1%C．99%D．99.9%（）121sinA30A121022yx22243234P(K2≥k0)0.1000.0500.0250.0100.001k02.7063.8415.0246.63510.8287．直线过椭圆的左焦点F1和一个顶点B，该椭圆的离心率为()A．25B．15C．2√55D．√558．过双曲线的一个焦点F2作垂直于实轴的直线，交双曲线于P、Q，F1是另一焦点，若∠21QPF，则双曲线的离心率e等于（）A．12B.2C.12D.229.设f'(x)是函数f(x)的导函数，y=f'(x)的图像如图，则y=f(x)的图像最有可能()10．函数f(x)＝x3－3x+1在区间[-3，0]上的最大值、最小值分别是（）A．1，－1B.3，-17C.1，－17D.9，－1911．设曲线y＝ax2在点(1,a)处的切线与直线2x－y－6=0平行,则a的值为()A.1B.C.D.－112．设函数在区间[a-1，a+1]上单调递减,则实数a的取值范围是()A.(1,2]B.[4,+∞)C.(－∞,2]D.(0,3]二、填空题（本大题共4小题，每小题5分，共20分）13．命题“若∠C=900，则ΔABC是直角三角形”与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是214．动圆M与圆C1：和圆C2：都外切，则动圆M圆心的轨迹方程是15．函数有极值的充要条件是16．对于椭圆x216+y29=1和双曲线x27−y29=1有以下4个命题，其中正确命题的序号是.①椭圆的焦点恰好是双曲线的顶点;②双曲线的焦点恰好是椭圆的顶点;③双曲线与椭圆共焦点;④椭圆与双曲线有两个顶点相同.3三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(12分)命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,q:函数f(x)=(3-2a)x是增函数,若p或q为真,p且q为假,求实数a的取值范围.18.(12分)已知椭圆的两焦点为F1(-√3,0),F2(√3,0),离心率.(1)求此椭圆的方程.(2)设直线l:y=x+m,若l与此椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.19.（12分）（1）椭圆中心在原点，焦点在x轴上，长轴长为18，且两个焦点恰好将长轴三等分，求此椭圆的方程.（2）求与椭圆＋＝1有公共焦点，且过点(－2，)的双曲线方程；420.（10分）求下列函数的导数(1)y=3x2−xsinx(2)y=lnxx+1−2x21.(12分)某商场从生产厂家以每件20元购进一批商品，若该商品零售价定为元，则销售量（单位：件）与零售价（单位：元）有如下关系：．问该商品零售价定为多少时毛利润最大，并求出最大毛利润（毛利润销售收入进货支出）．22.（12分)已知函数.(1)若的图象有与x轴平行的切线,求b的取值范围.(2)若在x=1处取得极值,且x∈[－1,2]时,f(x)1,解得a<1.因为p或q为真,p且q为假,所以p和q一真一假,若p真q假,则{−20,得m2<5(*).设P(x1,y1),Q(x2,y2),则x1+x2=－8m5,x1x2=4(m2−1)5,∴|PQ|=√2[(−8m5)2−16(m2−1)5]=2.解得m2=158,满足(*),所以m=±√304.619.（1）（2）20.（1）（2）21.解：由题意知，．令，得...