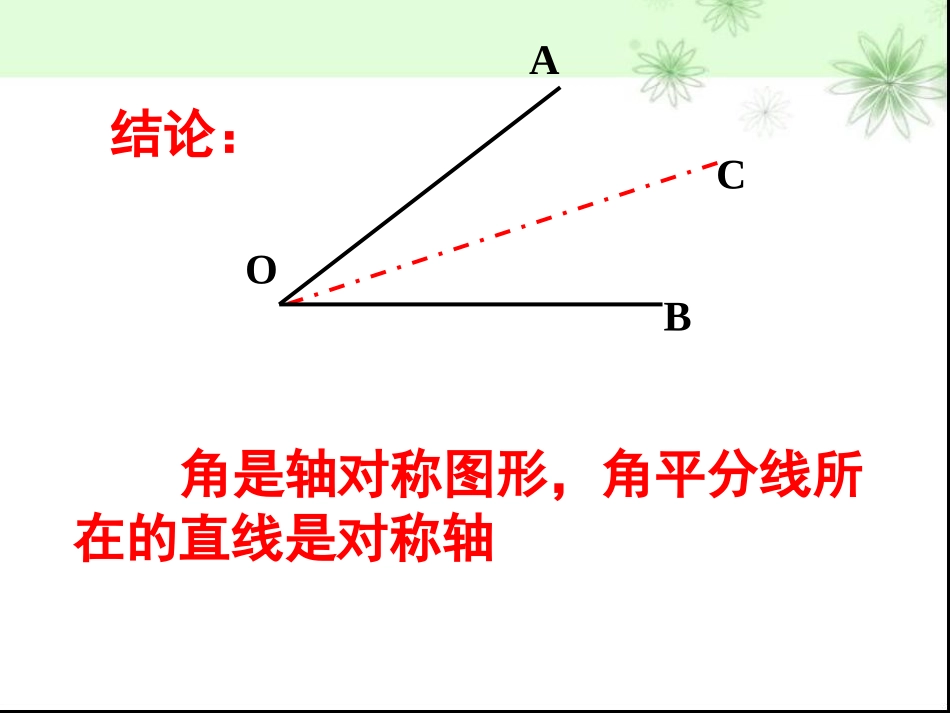
第五章生活中的轴对称5.3简单的轴对称图形(第3课时)ADBCEADCB不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?AOBC再打开纸片,再打开纸片,看看折痕与这个角有看看折痕与这个角有何关系?何关系?(对折)C结论:角是轴对称图形,角平分线所在的直线是对称轴ABO有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?对这种可以折叠的角可以用折叠方法得到角平分线,对不能折叠的角怎样得到其角平分线?证明:在△ACD和△ACB中AD=AB(已知)DC=BC(已知)CA=CA(公共边)∴△ACD≌△ACB(SSS)∴∠CAD=∠CAB(全等三角形的对应边相等)∴AC平分∠DAB(角平分线的定义)ADBCE根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)OABCENOMCENM2.分别以M,N为圆心.大于MN的长为半径作弧.两弧在∠AOB的内部交于C.21用尺规作角的平分线的方法用尺规作角的平分线的方法AABBOOMMNNCC作法:1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.3.作射线OC.则射线OC就是∠AOB的平分线.如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D、E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.PAOBCDEPD=PE角平分线上的点到这个角的两边的距离相等。已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵PDOA⊥,PEOB⊥(已知)∴∠PDO=PEO=90∠(垂直的定义)在△PDO和△PEO中∴PD=PE(全等三角形的对应边相等)∠PDO=PEO∠AOC=BOC∠∠OP=OP∴△PDOPEO≌△(AAS)DPEAOBC角平分线上的点到这个角的两边的距离相等.角平分线上的角平分线上的点到这个角两点到这个角两边的距离相等。边的距离相等。角平分线的性质:利用此性质怎样书写推理过程?一线,一点,两距离,两相等角平分线的性质定理:角平分线上的点到这个角的两边的距离相等。几何语言AOBPED12∵OP是∠AOB的平分线PD⊥OA,PE⊥OB∴PD=PE(角的平分线上的点到角的两边的距离相等)推理的理由有三个,必须写完整,不能少了任何一个。角平分线的性质角平分线上的点到这个角的两边的距离相等。BADOPEC定理应用所具备的条件:(1)角的平分线;(2)点在该平分线上;(3)垂直距离。定理的作用:证明线段相等。OABCEDP辨一辨如图,OC平分∠AOB,PD与PE相等吗?(1)∵如图,AD平分∠BAC(已知)∴=,()角平分线上的点到这个角的两边的距离相等。ADCBBDCD(×)(2)∵如图,DC⊥AC,DB⊥AB(已知)∴=,()角平分线上的点到这个角的两边的距离相等。ADCBBDCD(×)(3)∵AD平分∠BAC,DC⊥AC,DB⊥AB(已知)∴=,()DBDC角平分线上的点到这个角的两边的距离相等。ADCB√不必再证全等练一练1、如图,∵OC是∠AOB的平分线,又________________∴PD=PE(角的平分线上的点到角的两边的距离相等)))PDOA⊥,PEOB⊥BOACDPE2、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?ABCDE3、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.ADOBEPC44、已知△ABC中,∠C=900,AD平分∠CAB,且BC=8,BD=5,求点D到AB的距离是多少?ABCDE你会吗?5、已知:如图,在△ABC中,AD是它的角平分线且BD=CDB=C∠∠,DE⊥AB,DF⊥AC.垂足分别为E,F.求证:EB=FC.ABCDEF分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE≌Rt△CDF.课堂小结角平分线尺规作图属于基本作图,必须熟练掌握性质定理一个点:角平分线上的点;二距离:点到角两边的距离;两相等:两条垂线段相等辅助线添加过角平分线上一点向两边作垂线段回味无穷