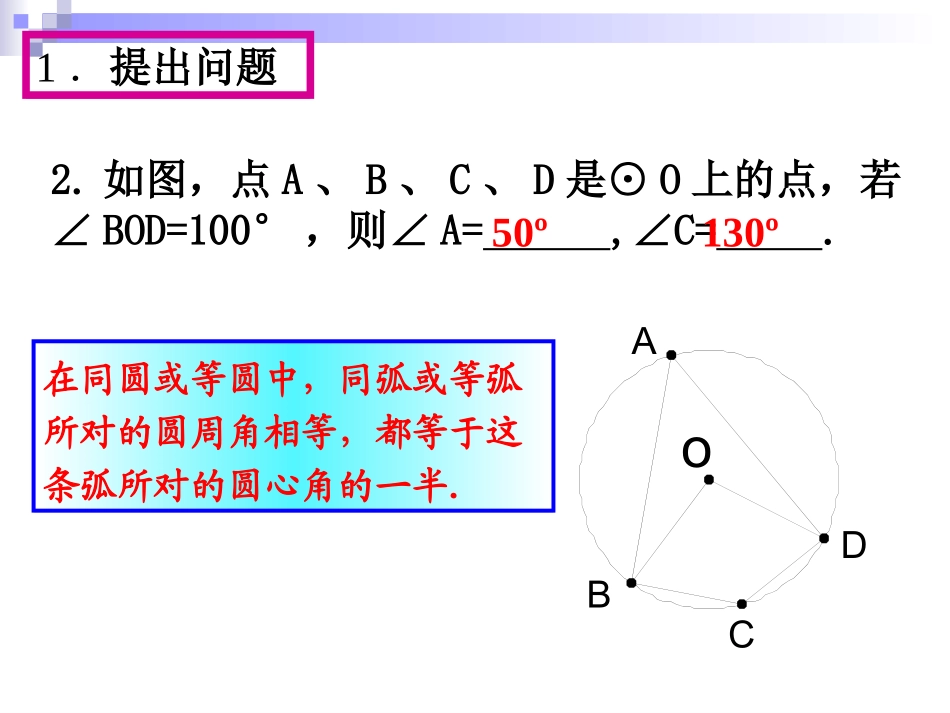
24.1圆的有关性质(第5课时)九年级上册马瑜1.如图,AB是⊙O的直径,C为圆上一点,则∠ACB=.oBcA半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.90º1.提出问题2.如图,点A、B、C、D是⊙O上的点,若∠BOD=100°,则∠A=,∠C=.oCBDA在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.50º130º1.提出问题什么叫圆内接三角形?什么叫圆内接四边形?1.提出问题观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?2.性质探究猜想:∠A与∠C,∠B与∠D之间的关为。∠A+∠C=180º;∠B+∠D=180ºOCDBA如图:已知圆内接四边形ABCD求证:∠A+∠C=180゜圆的内接四边形的对角互补。2.性质探究1.四边形ABCD是⊙O的内接四边形,且A=110°,∠B=80°,则∠C=_________,∠D=____.2.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3,则∠D=.70º100º90º3.利用性质解决问题如图,CD是△ABC的中线,且CD=AB.求证:∠ACB=90°.21DCBA证明:∵在△ABC中,CD是AB边上的中线∴AD=BD又∵CD=AB∴AD=BD=CD∴A、B、C在以点D为圆心,AB为直径的圆上。∴∠ACB=90°21结论:如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。3.利用性质解决问题1.四边形ABCD是⊙O的内接四边形,且∠BOD=110°,则∠C=.2.⊙O中,∠AOB=110°,则弦AB所对的圆周角的度数为.3.⊙O的内接四边形ABCD中∠A∶∠B∶∠C∶∠D可能是()A.1∶2∶3∶4B.4∶1∶3∶2C.4∶3∶1∶2D.4∶1∶2∶4125º55º或125ºC3.利用性质解决问题4.已知:□ABCD是⊙O的内接四边形,求证:□ABCD是矩形.3.利用性质解决问题(1)本节课主要学习了哪些内容?(2)本节课学到了哪些思想方法?①构造圆内接四边形;②一题多解,一题多变.4.课堂小结1.如下图左,四边形ABCD内接于⊙O,AB是直径,∠ABD=30°,则∠BCD的度数为多少?2.如下图右,在⊙O中,AB为直径,直线l与⊙O交于点C、D,BE⊥l于点E,连接BD、BC.求证:∠CBE=∠ABD.5.布置作业ABODCElABCDO