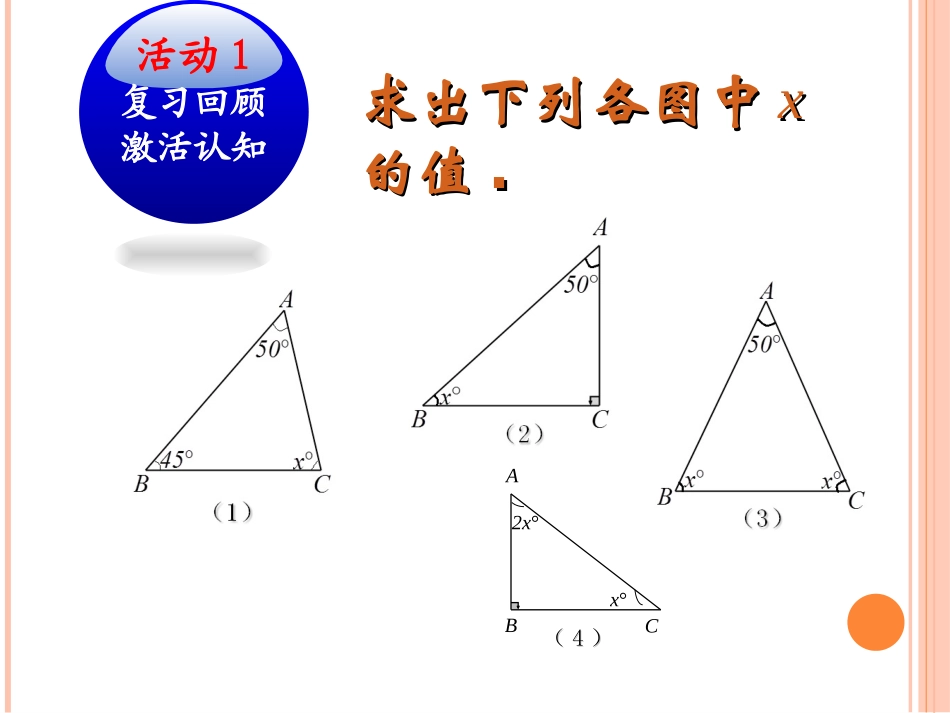
第十一章三角形11.2.111.2.1三角形的内角三角形的内角第第22课时课时11.211.2与三角形有关的角与三角形有关的角活动1复习回顾激活认知求出下列各图中求出下列各图中xx的值的值..x°2x°CBA((44))你能把下列推理补充完整吗?你能把下列推理补充完整吗?如图,在△ABC中,∠A+∠B+∠C=_____().∵∠C=90°(),∴∠A+∠B=_______.180°180°三角形内角和定理已知90°直角三角形的性质:两个锐角互余直角三角形的性质:两个锐角互余..BCA(1)如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.(2)如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.活动2尝试应用训练技能探究一:探究一:oDCBA((11))oDCBA((22))方法一(利用平行的判定和性质):∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.方法二(利用直角三角形的性质):∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.∵∠AOB=∠COD,∴∠A=∠D.第(第(11)题方法对比:)题方法对比:oDCBA(1)两个图形的相同点和不同点各是什么?(2)图(1)的两种解答方法能用于图(2)的解答吗?哪个更具一般性?设疑讨论:设疑讨论:oDCBA(1)oDCBA(2)如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD,BE相交于点F,∠ECF与∠DBF有什么关系?为什么?活动3深化提高巩固提升探究二:探究二:FEDCBA图4归纳总结:归纳总结:你能画出不同解题方法中包含的基本图形吗?FEDCBFEDCBA追问设疑:追问设疑:∠A与∠BFC又有什么关系?解:∵CD⊥AB于点D,BE⊥AC于点E,∴∠BEA=∠BDF=90°,∴∠ABE+∠A=90°,∠ABE+∠DFB=90°.∴∠A=∠DFB.∵∠DFB+∠BFC=180°,∴∠A+∠BFC=180°.尝试应用:尝试应用:如图,在△ABC中,∠A:∠B:∠C=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于H,求∠BHC的度数.HEDCBA图5活动4正反应用回归本质思考思考:在△:在△ABCABC中,若∠中,若∠AA+∠+∠BB=90°=90°,,你能判断它是什么三角形吗?请说出判你能判断它是什么三角形吗?请说出判断的依据断的依据..探究三:探究三:判断:判断:△△ABCABC是直角三角形是直角三角形..证明:∵∠证明:∵∠AA+∠+∠BB=90°=90°,,∴∠∴∠CC=180°-∠=180°-∠AA-∠-∠BB=90°.=90°.∴△∴△ABCABC是直角三角形(直角三角形定是直角三角形(直角三角形定义)义)..练习巩固:练习巩固:1.1.在△在△ABCABC中,若∠中,若∠AA:∠:∠BB:∠:∠CC==1:2:31:2:3,那么三角形是直角三角形吗?,那么三角形是直角三角形吗?2.2.在△在△ABCABC中,若∠中,若∠AA+∠+∠BB=∠=∠CC,那,那么三角形是直角三角形吗?么三角形是直角三角形吗?思考:两个角互余是直角三角形特有的思考:两个角互余是直角三角形特有的性质吗?性质吗?判定:有两个角互余的三角形是直角三判定:有两个角互余的三角形是直角三角形角形..简单应用:简单应用:在△ABC中,若∠A=43°,∠B=47°,你能判断这是什么三角形吗?方法一:∵∠C=180°-∠A-∠B=180°-43°-47°=90°,∴△ABC是直角三角形(直角三角形的定义).方法二:∵∠A+∠B=43°+47°=90°,∴△ABC是直角三角形(直角三角形的判定).本节课你学习了哪些知识?活动5课堂小结检测反馈小结与提升小结与提升::直角三角形角的特征;直角三角形的判定方法;与直角三角形相关的几个基本图形.活动5归纳小结深化新知小结与提升:小结与提升:直角三角形的两个锐角互余复杂图形中识别基本图形收收获获解决一些常见“相等角”的证明问题小结与提升:小结与提升:有两个角互余的三角形是直角三角形检测反馈:检测反馈:教材第14页练习第1、2题.