平面向量基本定理(公开课)VIP免费

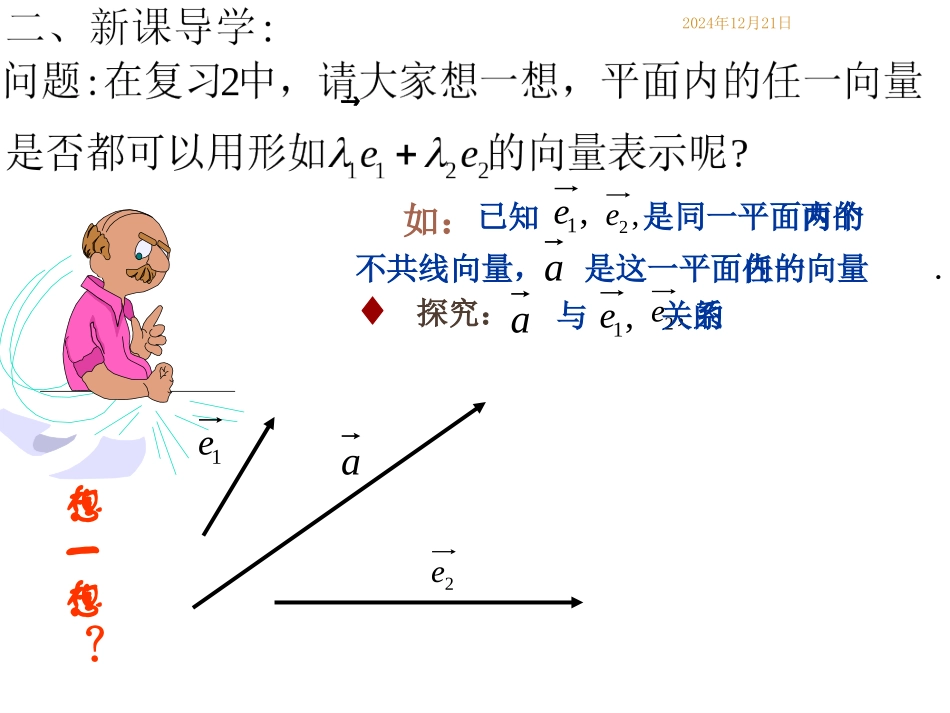
平平平平平平平平2024年12月21日(0),,.(a0,0b0aabbab向量与共线当且仅当有唯一一个实数使若当时，不唯一；当时，不存在）一、课前准备：:共线向量定理复习1:12122:,,3?eeee��复习给定平面内任意两个向量我们能否作出向量2向量的合成（思考：为什么限定？）0a1223dee��1e�2e�d�2024年12月21日想一想？♦探究：a与,1e,2e的关系1e2ea是这一平面内的任一向量．已知是同一平面内的两个,1e,2e不共线向量，a如：2024年12月21日学生活动：1e2eaOMNCONOMOCOBOA21即2211eea1e1e2e向量的分解AB2024年12月21日知识点一平面向量基本定理存在性唯一性,1e1.如果是同一平面内的两个不共线向量，那么对于这一平面的任意向量2e�,a使一对实数,2,12211eea有且只有把不共线的向量叫做表示这一平面内所有向量的一组基底12ee�２.平面向量基本定理的几点说明,0211122aee��使若a与)(21ee共线，则210(0),若0,a��则有且只有⑴（3）(2)定理的代数表达形式：若不共线，则21,ee��112212abeeee�12=ba且,021设是平面内的一组基底，当恒有11220ee�21,ee��1122aee��使2024年12月21日?思考1平面内用来表示一个向量的基底有多少组（有无数组）BAOMa1e2eOMaABxy2024年12月21日12,,?思考2、若基底选取不同则表示同一向量的实数是否相同BAOMa1e2eOMaABxy2123eeayxa423mnnma23知识小结：(1).基底的选择是不唯一的；(2).同一向量在选定基底后，12,是唯一存在的(3).同一向量在选择不同基底时，可能相同也可能不同12,1.//2,,,,ABCDABCDABCDDCBAADaABbabDCBCEF���例如图梯形中，，，E、F是，中点，，试以为基底表示abABDCFE知识点二、向量的夹角与垂直:OABba两个非零向量和,作，,则abAOB叫做向量和的夹角．OAa�OBb�ab夹角的范围：00180,0180与反向abOABab记作ab90与垂直，abOABab注意:两向量必须是同起点的0与同向abOABab特别的：例2.在等边三角形中，求(1)AB与AC的夹角；(2)AB与BC的夹角。ABC60'C0120本节小结再见