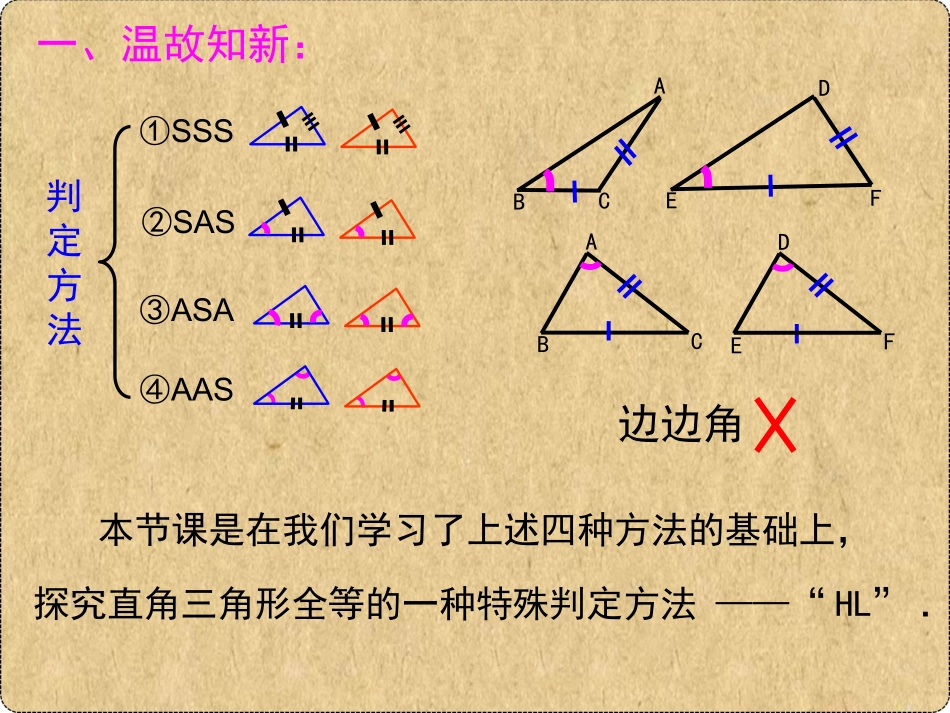
自学质疑温故知新合作探究展示反馈感悟自得12.2三角形全等的判定(五)(HL)•学习目标:1.探索并理解“HL”判定方法.2.会用“HL”判定方法证明两个直角三角形全等,并发展合情推理能力.一、温故知新:①SSS③ASA②SAS④AAS本节课是在我们学习了上述四种方法的基础上,探究直角三角形全等的一种特殊判定方法——“HL”.边边角ABECDFABCDEF判定方法二、自学质疑:斜边和一条直角边分别相等的两个直角三角形全等。ACBDFEH——Hypotenuse,斜边L——Leg,直角边HypotenuseLeg(HL)要求:阅读P41—42,划出重点,完成下列填空:ACBDFE和分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”).斜边一条直角边()在和中二、自学质疑:ACBDFE和分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”).斜边一条直角边二、自学质疑:直角三角形全等的判定:BC=EFAC=DF(HL)在Rt△ABC和Rt△DEF中④AAS①SSS③ASA②SAS判定方法⑤HL例5如图,AC⊥BC,BD⊥AD,AC=BD.求证:B=AD.三、合作探究:“HL”判定方法的运用“万能”证明法BC=AD△ABC≌△BADBADCABBADC①审题作标记②拆分三角形(可选)③两边往中间搭桥AC⊥BC,BD⊥ADAC=BDRt△ABC在和中Rt△BADRtRtBADCAD课本P44第7题四、展示反馈:CADB小组评分:(1)小组成员4人(含4人)以上正确作答,小组奖励4分。(2)板书展示的小组获2分。(3)发现错漏并改正的小组获2分。BDD课本P44第8题四、展示反馈:BAC(1)应用“HL”判定方法的前提条件是什么?(2)判定两个直角三角形全等有哪些方法?四、感悟自得:④AAS①SSS③ASA②SAS判定方法⑤HL思维导图≌AASSSSSAS全等条件ASAHL对应角对应边重合剥离平移翻折旋转变换“万能”证明法①审题作标记②拆分三角形(可选)③两边往中间搭桥格式:四、感悟自得:例5如图,AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.ABCD变式:如图,AC⊥BC,BD⊥AD,AD=BC.求证:△DAE≌△CBEABCDE拓展1:拓展2:已知:如图,AB=CD,CE=BF,AE⊥BC,DF⊥BC,求证:AE=DF自学质疑温故知新合作探究展示反馈感悟自得作业:《新课程》P27达标体验1-5、6*、7*