函数、极限、连续VIP免费

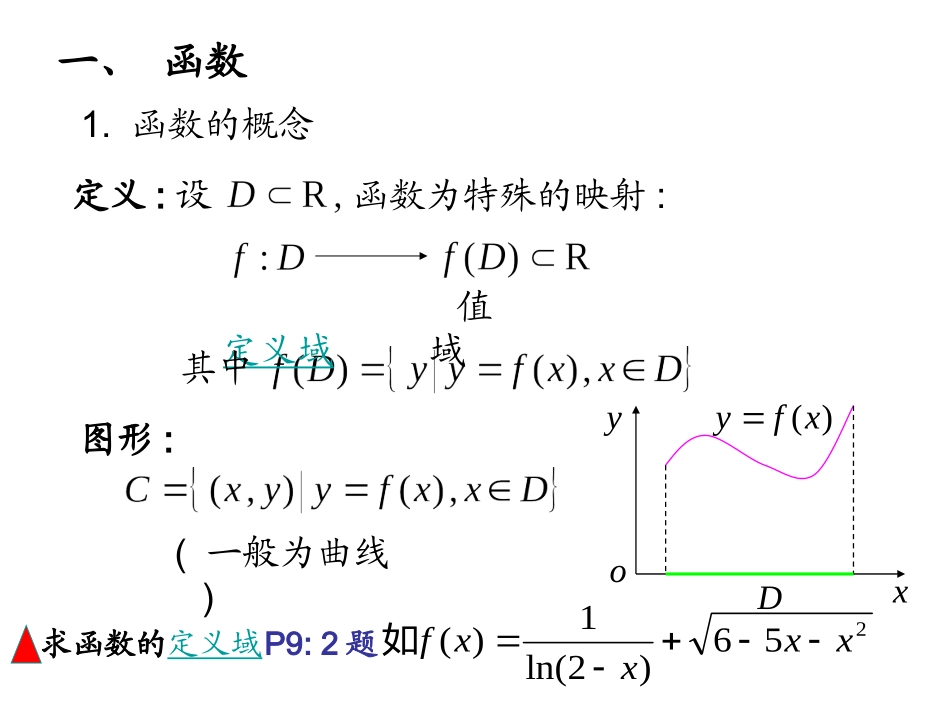
高等数学高等数学Highermathematics分析基础函数极限连续—研究对象—研究方法—研究桥梁函数、极限与连续高等数学高等数学Highermathematics函数的定义函数的定义反函数反函数反函数与直接函数之间关系反函数与直接函数之间关系基本初等函数基本初等函数复合函数复合函数初等函数初等函数函数的性质单值与多值奇偶性单调性有界性周期性函数的性质单值与多值奇偶性单调性有界性周期性双曲函数与反双曲函数双曲函数与反双曲函数第一章函数主要内容一、函数)(xfyyxoD1.函数的概念定义:定义域值域图形:(一般为曲线)设函数为特殊的映射:其中求函数的定义域P9:2题256)2ln(1)(xxxxf如2.函数的特性有界性,单调性,奇偶性,周期性3.反函数设函数为单射,反函数为其逆映射DDff)(:14.复合函数给定函数链则复合函数为])([:DgfDgf5.初等函数有限个常数及基本初等函数经有限次四则运算与复复合而成的一个表达式的函数.高等数学高等数学Highermathematics2.函数的几种特性设函数,,)(Dxxfy且有区间.DI(1)有界性,Dx,0M使,)(Mxf称)(xf,Ix,0M使,)(Mxf称)(xf说明:还可定义有上界、有下界、无界(2)单调性为有界函数.在I上有界.,Dx使若对任意正数M,均存在,)(Mxf则称f(x)无界.称为有上界称为有下界,)(,Mxf),(,xfM当,,21Ixx21xx时,,)()(21xfxf若称)(xf为I上的,)()(21xfxf若称)(xf为I上的单调增函数;单调减函数.xy1x2x如:y=1/x在(0,1)和),0(高等数学高等数学Highermathematicsxyoxx(3)奇偶性,Dx且有,Dx若则称f(x)为偶函数;若则称f(x)为奇函数.说明:若)(xf在x=0有定义,.0)0(f)(xf为奇函数时,则当必有定义域关于原点对称图像关于y轴对称图像关于原点对称高等数学高等数学Highermathematics(4)周期性,0,lDx且,Dlx则称)(xf为周期函数,xo2y2若称l为周期(一般指最小正周期).周期为周期为注:周期函数不一定存在最小正周期.例如,常量函数Cxf)(高等数学高等数学Highermathematics4.反函数与复合函数(1)反函数的概念及性质若函数为单射,则存在逆映射习惯上,Dxxfy,)(的反函数记成)(,)(1Dfxxfy称此映射1f为f的反函数.其反函数(减)(减).1)y＝f(x)单调递增且也单调递增性质:高等数学高等数学Highermathematics2)函数与其反函数的图形关于直线对称.例如,),(,xeyx对数函数互为反函数,它们都单调递增,其图形关于直线对称.)(xfyxy),(abQxyo指数函数高等数学高等数学Highermathematics(2)复合函数1),(Duufy1)(DDg且则设有函数链称为由①,②确定的复合函数,①—复合映射的特例②u称为中间变量.注意:构成复合函数的条件1)(DDg不可少.例如,函数链:,arcsinuy函数但函数链22,arcsinxuuy不能构成复合函数.可定义复合高等数学高等数学Highermathematics5.初等函数(1)基本初等函数(六大类)幂函数、指数函数、对数函数、三角函数、反三角函数(2)初等函数由基本初等函数否则称非初等函数.例如,33xxy构成,并可用一个式子表示的函数,经过有限次四则运算和复合步骤所称为初等函数.又如,双曲函数与反双曲函数也是初等函数.常数函数、高等数学高等数学Highermathematics初等函数2.幂函数3.指数函数5.三角函数1.常值函数4.对数函数6.反三角函数高等数学高等数学Highermathematics一、基本初等函数常值函数oxyCy1.常值函数constantfunctionCCy其中C是常数定义域值域),(}|{Cyy高等数学高等数学Highermathematics幂函数)(是常数xyoxy)1,1(112xyxyxy1xy2.幂函数(powerfunctions)定义域值域都过点(1,1)高等数学高等数学Highermathematicsxayxay)1(a)1,0()10(aaayx且3.指数(exponentialfunction)指数函数定义域值域),(),0(都过点(0,1)10a高等数学高等数学Highermathematics4.对数函数)1,0(logaaxyaxylnxyalogxyalog)1(a)0,1((logarithmicfunction)定义域值域),(),0(都过点(1,0)自然对数a=e=2.71828…时10a高等数学高等数学Highermathematics正弦函数xysinxysin5.三角函数定义域值域...