《理论力学》期中复习资料VIP免费

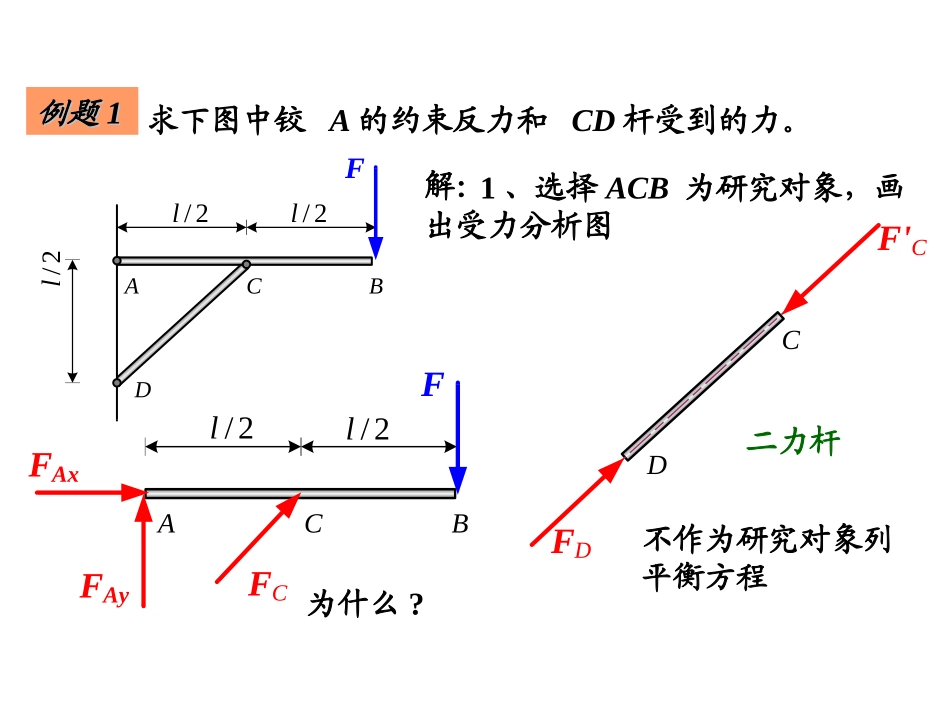
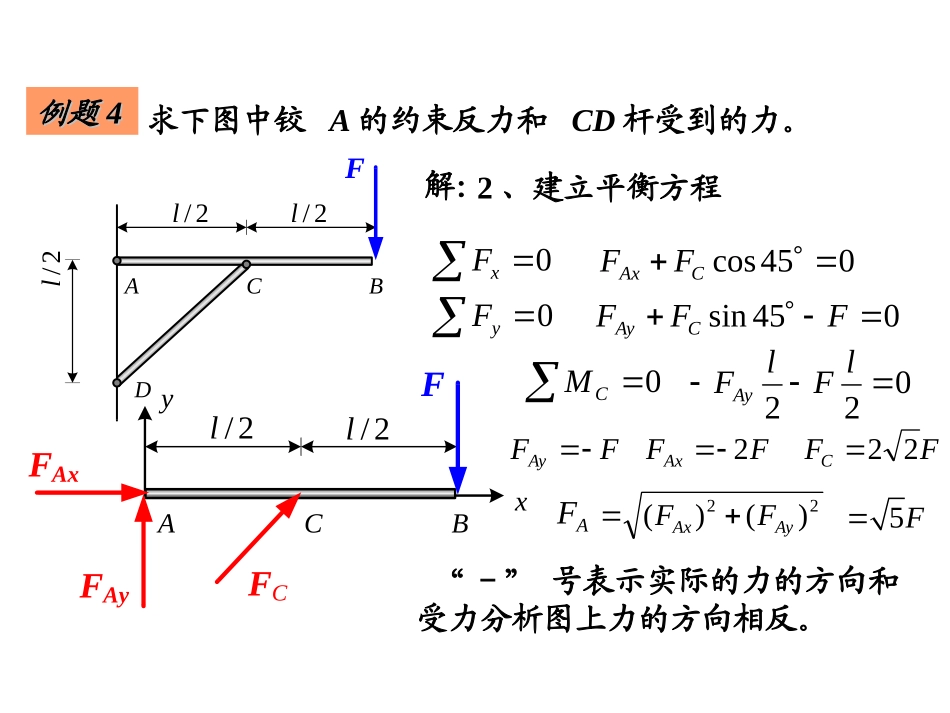
《理论力学》期中复习资料ACBD2/l2/l2/lF求下图中铰A的约束反力和CD杆受到的力。例题例题11解：1、选择ACB为研究对象，画出受力分析图ACB2/l2/lFFAxFAyFC为什么?CDFDF'C二力杆不作为研究对象列平衡方程ACBD2/l2/l2/lFxy0xF045cosCAxFF0yF045sinFFFCAy0CM022lFlFAyFFFFFFCAxAy222求下图中铰A的约束反力和CD杆受到的力。例题例题44解：2、建立平衡方程AF22)()(AyAxFF5F“－”号表示实际的力的方向和受力分析图上力的方向相反。ACB2/l2/lFFAxFAyFCACBD2/l2/l2/lF1、选择ACB作为研究对象，画出受力分析图ACB2/l2/lFFC45OFA解法2FFCFA45a2、画出平衡的力三角形45sinAFa90sinCFa45sinFFFFA545sin45sinaFFFC2245sin90sinaa例题2：横梁AB长l，A端用铰链杆支撑，B端为铰支座。梁上受到一力偶的作用，其力偶矩为M，如图所示。不计梁和支杆的自重，求A和B端的约束力。ABDM45llABMFBFA选梁AB为研究对象。lMlMFFBA245cos解得[解]045coslFMA,0M列平衡方程：AD是二力杆，A端的约束力必沿AD杆。力偶只能与力偶平衡，因此A与B端的约束力FA和FB构成一力偶，故有：FA=FB解：结点法先取整体为研究对象,受力如图所示。由平衡方程如图平面桁架，求各杆内力。已知铅垂力FC=4kN，水平力FE=2kN。aaaaaaaaFFCCAACCDDBBEEFFFFEE0AxEFF0x，0BAyCFFF0,y30CEBFaFaFa0,AMFAx=－2kNFAy=2kNFB=2kNaaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAx联立求解得例题3取结点A，受力分析如图。由平衡方程解得22kN,NAFF4kNNACFFAxFAyAFNACFNAFFNFEFNFAFNFCFF解得2kN，NFEF2kNNFCFcos450AxNACNAFFFF0,xcos450AyNAFFF0,y0,xcos450NFENFAFF0,ycos450NFCNFAFF取结点F，受力分析如图。由平衡方程aaaaaaaaPPCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAxFAx=－2kNFAy=2kNFB=2kNFNCFFNCAFCCCFNCDFNCEcos450NCANCDNCEFFF0,xcos450CNCFNCEFFF0,y取结点C，受力分析如图。由平衡方程解得22kN,NCEF2kNNCDFaaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAxFAx=－2kNFAy=2kNFB=2kNFNDEFNDCDDFNDB0NDBNDCFF0,x0NDEF0,y解得3kN,NDBF0NDEF取结点D，受力分析如图。由平衡方程aaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAxFAx=－2kNFAy=2kNFB=2kNFBBBFNBDFNBE22kNNBDF22kNNBEF解得cos450NBDNBEFF0,x0,ycos450BNBEFF取结点B，受力分析如图。由平衡方程aaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAxFAx=－2kNFAy=2kNFB=2kN如图平面桁架，求FE，CE，CD杆内力。已知铅垂力FC=4kN，水平力FE=2kN。截面法解：先取整体为研究对象,受力如图所示。由平衡方程aaaaaaaaFFCCAACCDDBBEEFFFFEEaaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAx0AxEFF0x，0BAyCFFF0,y30CEBFaFaFa0,AMFAx=－2kNFAy=2kNFB=2kN联立求解得由平衡方程作一截面m-m将三杆截断，取左部分为分离体，受力分析如图。联立求解得22kN,NCEF2kN,NCDF2kNNFEFcos450NCDAxNFENCEFFFFcos450AyCNCEFFF0NFEAyFaFa0,x0,y0,CMFFNNFEFEFFNNCDCDaaFFCCAACCFFFFAAFFAADDEEFFNNCCEEmmaaaaaaaaFFCCAABBDDCCEEFFFFEEFFAyAyFFBBFFAxAxmmxyzABCDE3030G例4均质长方形板ABCD重G=200N，用球形铰链A和碟形铰链B固定在墙上，并用绳EC维持在水平位置，求绳的拉力和支座的反力。xyzABCDE3030GAXAYAZTBXBZ030sin:0)(21ABGABZABTFmBx030sin:0)(21ADTADGFmy0:0)(ABXFmBz解：以板为研究对象，受力如图，建立如图所示的坐标。xyzABCDE3030GAXAYAZTBXBZ030sin30cos:0TXXXBA030cos:02TYYA030sin:0GTZZZBA解之得：0BBZXNT200NXA6.86NYA150NZA100如图所示，计算均质组合体的重心位置的坐标...