大学物理第11章习题课选讲例题VIP免费

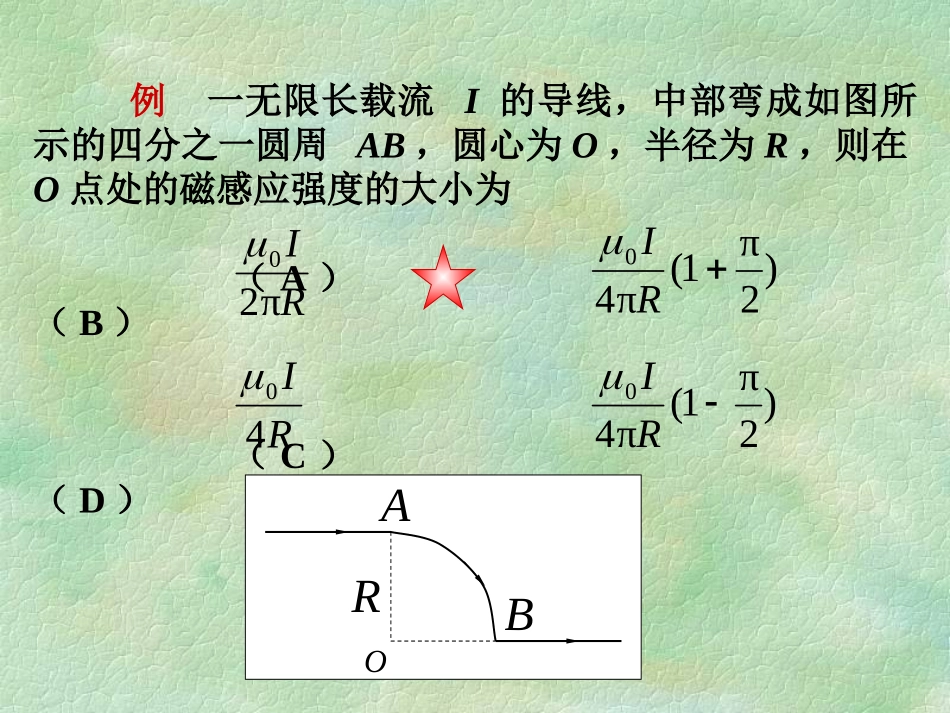
例一无限长载流I的导线，中部弯成如图所示的四分之一圆周AB，圆心为O，半径为R，则在O点处的磁感应强度的大小为（A）（B）（C）（D）RBAORIπ20)2π1(π40RIRI40)2π1(π40RI例一长直载流I的导线，中部折成图示一个半径为R的圆，则圆心的磁感应强度大小为（A）（B）（C）（D）0RORI20RIπ20RIRIπ2200例如图所示，四条皆垂直于纸面“无限长”载流直导线，每条中的电流均为I.这四条导线被纸面截得的断面组成了边长为2a的正方形的四个顶角，则其中心点O的磁感应强度的大小为（A）（B）（C）0（D）02πIa022πIa0πIaO2a例图中有两根“无限长”载流均为I的直导线，有一回路L，则下述正确的是（A），且环路上任意一点（B），且环路上任意一点（C），且环路上任意一点（D），且环路上任意一点常量ILI0dLlB0B0dLlB0B0dLlB0B0dLlBB例取一闭合积分回路，使三根载流导线穿过它所围成的面，现改变三根导线之间的相互间隔，但不越出积分回路，则：（）LB(1)回路内的不变，上各点的不变.(2)回路内的不变，上各点的改变.(3)回路内的改变，上各点的不变.(4)回路内的改变，上各点的改变.ILLBILLBILLBILL例边长为的正方形线圈，分别用图示两种方式通以电流（其中、与正方形共面），在这两种情况下，线圈在其中心产生的磁感强度的大小分别为：（）lI(1)(2)(3)(4)0,021BBabcdlIBBπ22,00210,π22201BlIBlIBlIBπ22,π220201III1B2Bcdab例如图，流出纸面的电流为，流进纸面的电流为，则下述各式中哪一个是正确的?（）I2(1)(2)(3)(4)IlBL02d1IIlBL02dIlBL03dIlBL04dI2I1L2L3L4L例在均匀磁场中，有两个平面线圈，其面积A1=2A2，通有电流I1=2I2，它们所受到的最大磁力矩之比M1/M2等于（A）1（B）2（C）4（D）1/4例一带电粒子，垂直射入均匀磁场，如果粒子质量增大到2倍，入射速度增大到2倍，磁场的磁感应强度增大到4倍，则通过粒子运动轨道包围范围内的磁通量增大到原来的（A）2倍（B）4倍（C）1/2倍（D）1/4倍例：电流均匀地流过宽度为b的无限长平面导体薄板，电流为I，沿板长方向流动。求：IPbb.在薄板平面内，距板的一边为b的P点处的磁感应强度；解：Ibd=Ixdπ2x0Bd=Idπ2b0=Ixxd2Bπ2b0=Ixxdbb=π2b0Iln2IPbb.xxd例半径为R的木球上绕有细导线，所绕线圈很紧密，相邻的线圈彼此平行地靠着，以单层盖住半个球面，共有N匝。如图所示。设导线中通有电流I。求：在球心O处的磁感应强度。2R2Iy2()+0Bd=x232y2Nd解：πNdNd=2=yRcosRsin=x=πNdIy2()+0x232y2+=πNdI()032RcosRcosRsin222222=πNdI0cosR22π=BπNdI0cosR20=NI0R4xyxydoR例在半径为R的无限长金属圆柱体内挖去一半径为r无限长圆柱体，两圆柱体的轴线平行，相距为d,如图所示。今有电流沿空心柱体的的轴线方向流动，电流I均匀分布在空心柱体的横截面上。分别求圆柱轴线上和空心部分轴线上的磁感应强度的大小；aRdrOO解：××××××××××××××××××××××××××××××××××....Rdroo运用补偿法解题：令小圆柱体通有等量反向电流，电流密度和大柱体相同。O点的磁场等于大柱体电流（横截面上全部通有电流）的磁场和小柱体反向电流磁场的叠加。小圆柱体的电流在O点的磁感应强度为零，磁场。所以O的磁场等于大圆柱体电流在该点的大柱体的电流在O点的磁感应强度为零，所以O点的磁场等于小柱体反向电流在O点所产生的磁场。××××××××××××××××××××××××××××××××××....RdrooRo解法一圆电流的磁场rrrrIddπ2π2drrIBd22dd00B,0向外例半径为的带电薄圆盘的电荷面密度为,并以角速度绕通过盘心垂直于盘面的轴转动，求圆盘中心的磁感强度.Rrrd2d2000RrBR,0向内B解法二运动电荷的磁场200dπ4drqBvrrqdπ2drvrBd2d02d2000RrBRRorrd例：一长...