中考复习二次函数图形及性质VIP免费

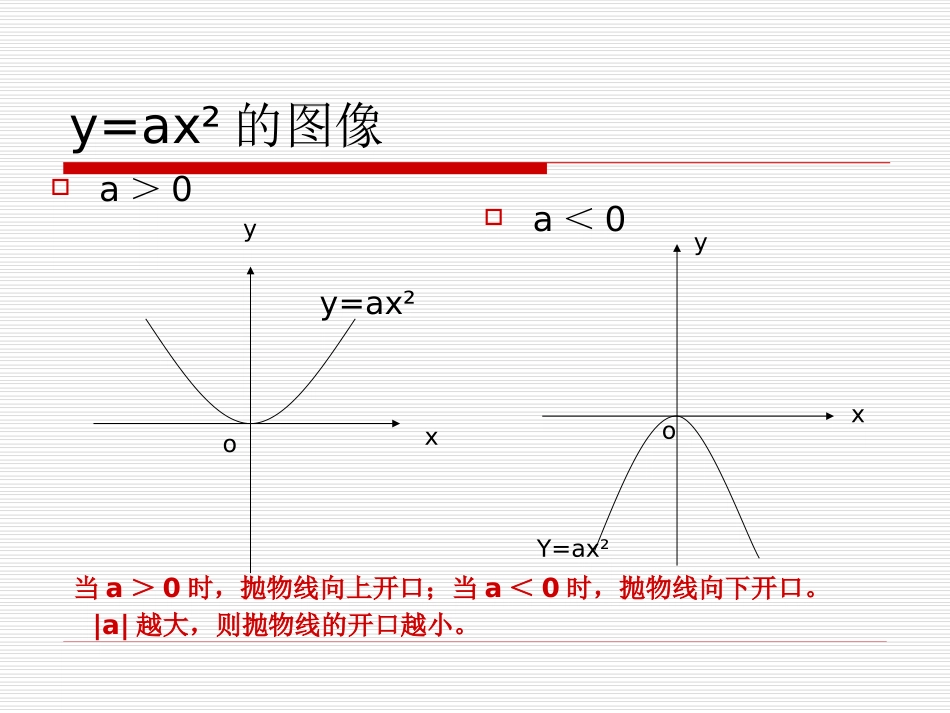
中考复课专题二次函数图像及性质大明中学张超峰y=ax²的图像a＞0a＜0y=ax²xyY=ax²yxoo当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口。|a|越大，则抛物线的开口越小。Y=ax²的性质a﹥0时图像开口向上关于y轴(直线x=0)对称顶点在原点对称轴左边y随x增大而减小；对称轴右边y随x增大而增大函数有最小值；最小值为0a﹤0时图像开口向下关于y轴(直线x=0)对称顶点在原点对称轴左边y随x增大而增大；对称轴y右边随x增大而减小.函数有最大值；最大值为0Y=a(x-h)²的图像y=ax²Y=a(x-h)²Y=a(x-h)²Y=a(x-h)²实际上是把Y=ax²的图像向右（或向左）平移|h|个单位。当h>0时，Y=a(x-h)²的图象可由抛物线Y=ax²向右平行移动h个单位得到，当h<0时，则向左平行移动|h|个单位得到．xyohhY=a(x-h)²的性质a﹥0时图像开口向上关于直线x=h对称顶点在（h，0）对称轴左边y随x增大而减小；对称轴右边y随x增大而增大函数有最小值；最小值为0a﹤0时图像开口向下关于直线x=h对称顶点在（h，0）对称轴左边y随x增大而增大；对称轴y右边随x增大而减小.函数有最大值；最大值为0Y=ax²+k的图象a＞0a＜0想一想，做一做。y=ax²xoy=ax²+k（k＞0）y=ax²+k（k＜0）Y=ax²+k实际上是把Y=ax²的图像向上（或向下）平移|k|个单位。(k＞0时向上；k＜0时向下)yY=ax²+k的性质a﹥0时图像开口向上关于y轴对称顶点在（0，k）对称轴左边y随x增大而减小；对称轴右边y随x增大而增大函数有最小值；最小值为ka﹤0时图像开口向下关于y轴对称顶点在（0，k）对称轴左边y随x增大而增大；对称轴y右边随x增大而减小.函数有最大值；最大值为kY=a(x-h)²+k的图像Y=a(x-h)²+k的图像是Y=ax²经过两次平移得到。Y=a(x-h)²Y=ax²Y=ax²+k当k>0时，向上平行移动k个单位；当k<0时，则向下平行移动个k单位。当h>0时，向右平行移动h个单位；当h<0时，则向左平行移动|h|个单位．xyY=a(x-h)²+k的性质a﹥0时图像开口向上关于直线x=h对称顶点在(h，k)对称轴左边y随x增大而减小；对称轴右边y随x增大而增大函数有最小值；最小值为ka﹤0时图像开口向下关于直线x=h对称顶点在(h，k)对称轴左边y随x增大而增大；对称轴y右边随x增大而减小.函数有最大值；最大值为kY=ax²+bx+c的图像因为Y=ax²+bx+c=a（x+b/2a)²+(4ac-b2/4a)即h=-b/2a;k=4ac-b2/4a，因而Y=ax²+bx+c的图像可以由Y=ax²平移两次得到xyY=ax²Y=ax²+bx+c=a（x+b/2a)²+(4ac-b2/4a)Y=ax²+(4ac-b2/4a)oX=-b/2aY=ax²+bx+c的性质a﹥0时，图像开口上；关于直线x=-b/2a对称顶点在(-b/2a，4ac-b2/4a)对称轴左边y随x增大而减小；对称轴右边y随x增大而增大函数有最小值；最小值为4ac-b2/4aa﹤0时，图像开口向下关于直线x=-b/2a对称顶点在(-b/2a，4ac-b2/4a)对称轴左边y随x增大而增大；对称轴y右边随x增大而减小.函数有最大值；最大值为4ac-b2/4a求抛物线的顶点、对称轴和最值的方法①配方法：将解析式化为Y=a(x-h)²+k的形式，顶点坐标为（h，k），对称轴为直线x＝h；若a＞0，y有最小值，且x＝h时，y最小=k；若a＜0，y有最大值，且x＝h时，y最大=k。②公式法：直接利用顶点坐标公式（-b/2a，4ac-b2/4a），求其顶点；对称轴是直线x=-b/2a若a＞0，y有最小值，且x＝-b/2a时，y最小=4ac-b2/4a；若a＜0，y有最大值，且x＝-b/2a时，y最大=4ac-b2/4a抛物线与x轴交点情况：对于抛物线Y=ax²+bx+c(△=b²-4ac)①当△﹥0时，抛物线与x轴有两个交点，反之也成立。②当△=0时，抛物线与x轴有一个交点，反之也成立，此交点即为顶点。③当△﹤0时，抛物线与x轴无交点，反之也成立。课堂小结：y=ax²的图像及性质Y=a(x-h)²的图像及性质Y=a(x-h)²+k的图像及性质Y=ax²+bx+c的图像及性质求抛物线的顶点、对称轴和最值的方法抛物线与x轴交点情况