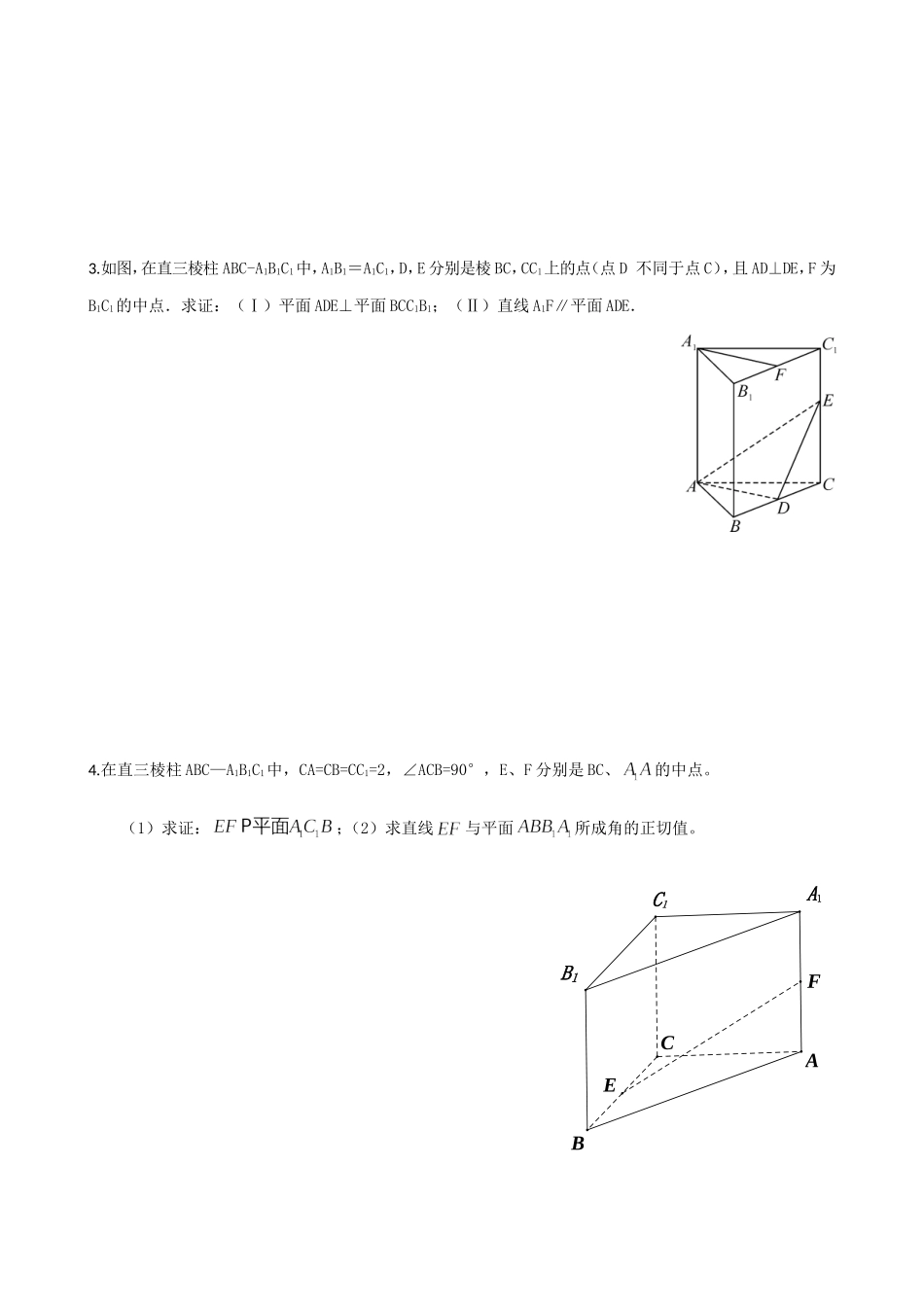
立体几何练习题1.如图,在三棱柱中,⊥底面,且△为正三角形,,为的中点.(1)求证直线∥平面;(2)求证平面⊥平面;(3)求三棱锥的体积.2.如图所示几何体是正方体截去三棱锥后所得,点为的中点。(1)求证:平面;(2)当正方体棱长等于时,求此几何体的体积。DB1C1ABCA13.如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:(Ⅰ)平面ADE⊥平面BCC1B1;(Ⅱ)直线A1F∥平面ADE.4.在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC、的中点。(1)求证:;(2)求直线与平面所成角的正切值。C1B1A1FECAB5.如图,在四棱锥PABCD中,PA平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,2,60ABBAD.(1)求证://OM平面PAB;(2)平面PBD平面PAC(3)当四棱锥ABCDP的体积等于3时,求PB的长.6.如图甲,在平面四边形ABCD中,已知,现将四边形ABCD沿BD折起,使平面ABD平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.(1)求证:DC平面ABC;(2)设,求三棱锥A-BFE的体积.7.如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,,点F是PB的中点,点E在边BC上移动.(Ⅰ)若,求证:;(Ⅱ)若二面角的大小为,则CE为何值时,三棱锥的体积为?8.如图,多面体中,两两垂直,且,,,.(Ⅰ)若点在线段上,且,求证:平面;(Ⅱ)求证:(Ⅲ)求直线与平面所成的角的正弦值.PABCDEF9.如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(I)求证:平面AEC⊥平面PDB;(II)当PD=AB且E为PB的中点时,求AE与平面PDB所成的角的大小.10.如图,菱形ABCD的边长为4,60BAD,ACBDO.将菱形ABCD沿对角线AC折起,得到三棱锥BACD,点M是棱BC的中点,22DM.(1)求证://OM平面ABD;(2)求证:平面DOM平面ABC;(3)求三棱锥BDOM的体积.11.如图在直三棱柱中,,是的中点,且交于点,点在线段上,.(1)证明:平面;(2)若直线平面,求直线与平面所成角的余弦值.12.如图,PA平面ABCD,四边形ABCD为矩形,PA=AB=3,AD=1,点F是PB的中点,点E在边BC上移动.(1)当点E为BC的中点时,证明EF//平面PAC;(2)求三棱锥E-PAD的体积;(3)证明:无论点E在边BC的何处,都有PEAF.13.长方体中,,,是底面对角线的交点。(Ⅰ)求证:平面;(Ⅱ)求证:平面;(Ⅲ)求三棱锥的体积。14.如图,已知在四棱锥中,底面是矩形,平面,、分别是、的中点,若二面角P-CD-A为,且.(Ⅰ)求证:平面;(Ⅱ)求异面直线PC与AB所成角的大小;(Ⅲ)求点到平面的距离.DCABPEF15.已知在四棱锥中,,,,分别是的中点.(Ⅰ)求证;(Ⅱ)求证;(Ⅲ)若,求二面角的大小.16.三棱柱中,侧棱与底面垂直,,,点分别为和的中点(1)证明:平面;(2)求三棱锥的体积;(3)证明:平面B1A1MABCNC1GHFABCDE17.如图组合体中,三棱柱111ABCABC的侧面是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合一个点.(1)求证:无论点C如何运动,平面1ABC平面1AAC;(2)当点C是弧AB的中点时,求四棱锥111ABCCB与圆柱的体积比.18.如图,在多面体ABDEC中,AE平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。(I)求证:EF//平面ABC;(II)求证:EF平面BCD;(III)求多面体ABDEC的体积。19.如右图,将一副三角板拼接,使它们有公共边,且使两个三角板所在平面互相垂直,若,,,.(Ⅰ)求证:平面平面.(Ⅱ)求二面角的平面角的余弦值.(Ⅲ)求到平面的距离.20.在三棱拄111ABCABC中,AB侧面11BBCC,已知11,3BCBCC,21CCAB.(Ⅰ)求证:1CBABC平面;(Ⅱ)试在棱1CC(不包含端点1,)CC上确定一点E的位置,使得1EAEB;(Ⅲ)在(Ⅱ)的条件下,求AE和平面ABC所成角正弦值的大小.ABCDEC1B1A1CBA试卷答案1.(1)见解析;(2)见解析;(3)9解析:(1)证明:连接B1C交BC1于点O,连接OD,则点O为B1C的中点.…………1分 D为AC中点,得DO为中位线,∴.…………………………2分∴直线AB1∥平面BC1D………………………4分(2)证明: 底面,∴……………………………………5分 底面正三角形,D是AC的中点∴...