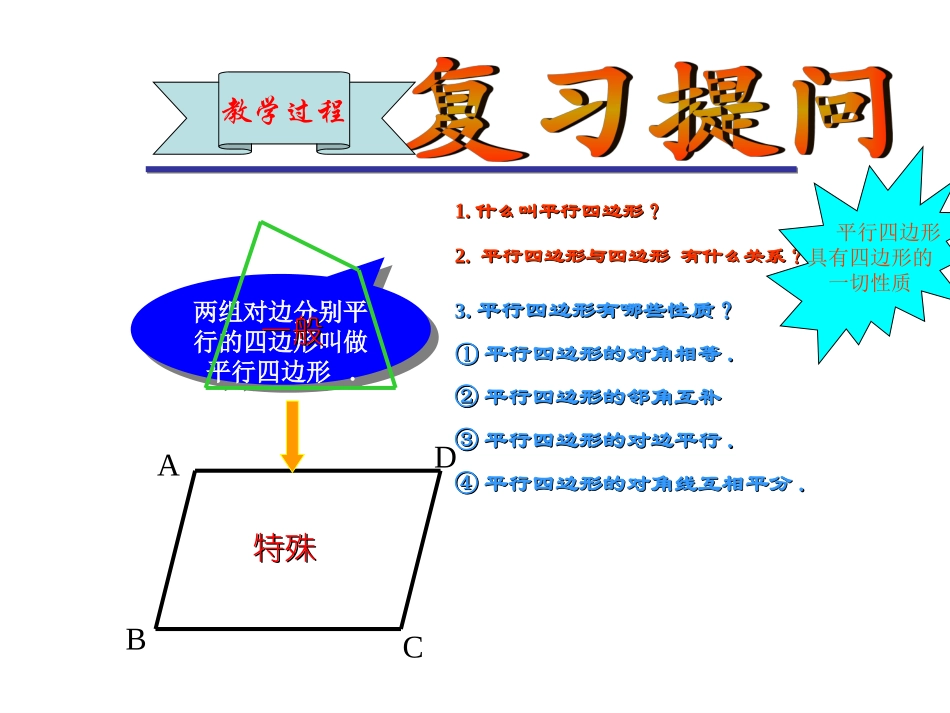
(二)教学目标1、知识与技能依据是:新课标对学生数学学习的总体目标规定“获得适应未来社会生活和进一步发展所必需的重要数学知识”。(2)、能熟练地运用矩形性质来解决问题(1)、掌握什么样的图形是矩形、矩形的性质教材分析1.1.什么叫平行四边形?什么叫平行四边形?33..平行四边形有哪些性质?平行四边形有哪些性质?①①平行四边形的对角相等平行四边形的对角相等..②②平行四边形的邻角互补平行四边形的邻角互补③③平行四边形的对边平行平行四边形的对边平行..④④平行四边形的对角线互相平分平行四边形的对角线互相平分..2.2.平行四边形与四边形有什么关系?平行四边形与四边形有什么关系?ABCD两组对边分别平行的四边形叫做平行四边形.两组对边分别平行的四边形叫做平行四边形.特殊特殊一般一般平行四边形具有四边形的一切性质教学过程矩形的定义及性质一个角是直角定义:有一个角是直角的平行四边形叫做矩形矩形平行四边形性质定理1矩形的四个角都是直角性质定理2矩形的对角线相等★矩形性质角边对角线对称性推论:直角三角形斜边上的中线等于斜边的一半★例1练习小结四个角都是直角对边平行且相等互相平分且相等是轴对称图形ABCD已知:矩形ABCD求证:AC=BD证明:在矩形ABCD中∵∠ABC=DCB=90°∠()AB=DC,BC=CB∴△ABCDCBAC=BD≌△∴?返回推论:直角三角形斜边上的中线等于斜边的一半已知△ABC中∠ACB=90°,AD=BD求证:CD=AB21证明:延长CD到E使DE=CD,连结AE、BE.ABCD∵AD=BD,CD=ED∴ACBE是平行四边形E又∵∠ACB=90°∴ACBE是矩形∴CE=AB()由于CD=CE所以CD=AB2121?返回例1已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB=4cm.求矩形对角线的长解:∵四边形ABCD是矩形∴OA=OD()∵∠AOD=120°∴∠1=30°又∵∠ABC=90°()∴BD=2AB=2×4=8cmABCDO1AC=BDOA=AC21OD=BD21?返回2.过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是课堂练习1.下面性质中,矩形不一定具有的是A.对角线相等B.四个角都相等C.是轴对称图形D.对角线垂直A.对角线相等的四边形B.对角线互相平分且相等的四边形C.对角线互垂直平分的四边形D.对角线垂直的四边形3.已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为A.50°B.60°C.70°D.80°4.矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于A.30°B.45°C.60°D.120°[][][][]DDDA返回A:四边形集合C:平行四边形集合B:矩形集合ACB课堂小结两组对边分别平行一个角是直角平行四边形矩形返回谢谢