平面向量的正交分解和坐标表示第二课时用VIP免费

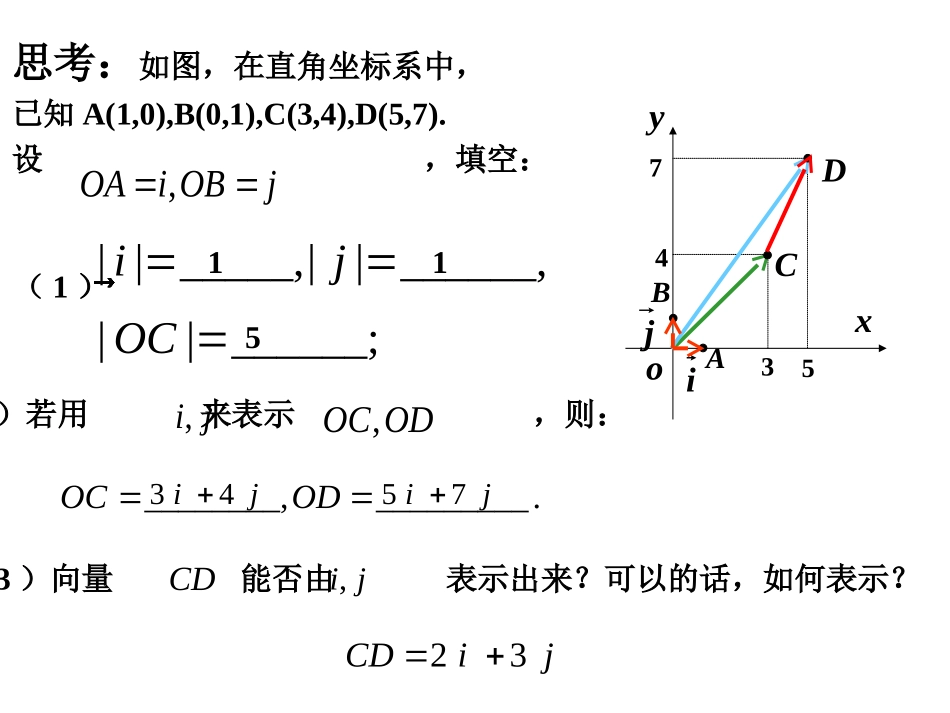
自主学习完成下列问题。1.什么是向量的正交分解。2.什么是向量的坐标表示。回顾：平面向量基本定理。12121122+eeaaee���如果、是同一平面内的两个线的向量，那么对于这一平面内的任一向量，有且只有一对实数、，可使不共把一个向量分解为两个互相垂直的向量，叫做把向量正交分解.如图，向量i、j是两个互相垂直的单位向量，向量a与i的夹角是30°，且|a|=4，以向量i、j为基底，向量a如何表示？BaiOjAP232aijABCDoxyij思考：如图，在直角坐标系中，已知A(1,0),B(0,1),C(3,4),D(5,7).设，填空：,OAiOBj�（1）||_____,||______,||______;ijOC�（2）若用来表示，则：,ij,OCOD�________,_________.OCOD�34ij�57ij�1153547（3）向量能否由表示出来？可以的话，如何表示？CD�,ij23CDij�在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量i、j作为基底，对于平面内的一个向量a，由平面向量基本定理知，有且只有一对实数x、y，使得a＝xi＋yj.我们把有序数对（x，y）叫做向量a的坐标，记作a＝(x，y).其中x叫做a在x轴上的坐标，y叫做a在y轴上的坐标，上式叫做向量的坐标表示.xyaiOjxy思考相等向量的坐标必然相等，作向量a，则(x，y)，此时点A的坐标是什么？OA�OA�AaixyOjA(x,y)例1如图，写出向量a，b，c，d的坐标.2452abcd－4－2－5－2xyOa=(2,3)b=(-2,3)c=(-2,-3)d=(2,-3)理论迁移探究（二）：平面向量的坐标运算思考1：设i、j是与x轴、y轴同向的两个单位向量，若a=(x1，y1),b=(x2，y2),则a＝x1i＋y1j，b＝x2i＋y2j，根据向量的线性运算性质，向量a＋b，a－b，λa（λR∈）如何分别用基底i、j表示？a＋b＝(x1＋x2)i＋(y1＋y2)j，a－b＝(x1－x2)i＋(y1－y2)j，λa＝λx1i＋λy1j.思考2：根据向量的坐标表示，向量a＋b，a－b，λa的坐标分别如何？a＋b＝(x1＋x2，y1＋y2);a－b＝(x1－x2，y1－y2);λa＝(λx1，λy1).a＋b＝(x1＋x2)i＋(y1＋y2)j，a－b＝(x1－x2)i＋(y1－y2)j，λa＝λx1i＋λy1j.思考3：如何用数学语言描述上述向量的坐标运算？两个向量和（差）的坐标分别等于这两个向量相应坐标的和（差）；实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.a＋b＝(x1＋x2，y1＋y2);a－b＝(x1－x2，y1－y2);λa＝(λx1，λy1).例已知a=(2,1),b=(－3,4),求a＋b，a－b，3a＋4b的坐标.a＋b＝(－1，5)，a－b＝(5，－3)，3a＋4b＝(－6，19).oxyBAAB�思考4：如图,已知点A(x1,y1),B(x2,y2)，那么向量的坐标如何？一般地，一个任意向量的坐标如何计算？＝(x2－x1，y2－y1).AB�任意一个向量的坐标等于表示该向量的有向线段的终点坐标减去始点坐标.思考：若向量a=(x，y)，则|a|如何计算？若点A(x1,y1)，B(x2，y2)，则如何计算？AB�222121AB(xx)(yy)�AaxyO22xya例4.如图，已知的三个顶点A、B、C的坐标分别是（-2，1）、（-1，3）、（3，4），试求顶点D的坐标。ABCDABCDxyO解法１：设点D的坐标为（x,y）(1,3)(2,1)(1,2)(3,4)(,)(3,4)ABDCxyxyABDC���且(1,2)(3,4)xy1324xy解得x=2,y=2所以顶点D的坐标为（2，2）ABCDxyO解法2：由平行四边形法则可得(2(1),13)(3(1),43)(3,1)BDBABC�而(1,3)(3,1)(2,2)ODOBBD�所以顶点D的坐标为（2，2）