整式的概念复习课VIP免费

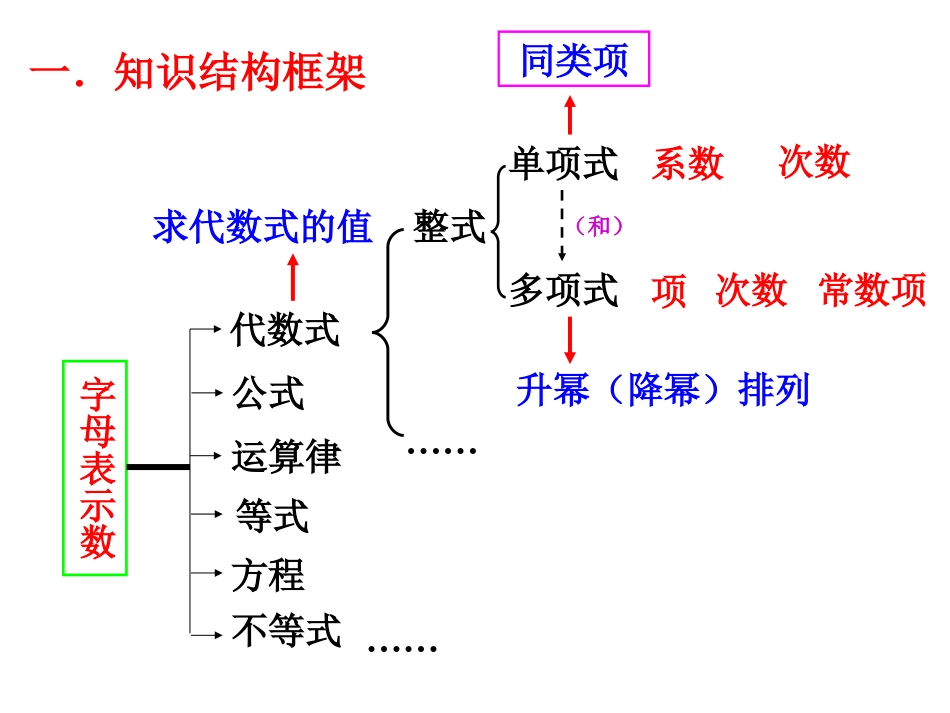
代数式方程不等式…………求代数式的值整式单项式多项式系数次数升幂（降幂）排列项次数常数项一．知识结构框架同类项（和）运算律字母表示数公式等式例1观察下列式子，指出哪些式子是代数式．二．知识应用102r1102r10221x35xxx352yx335xy3x代数式代数式方程代数式代数式代数式代数式不等式方程用运算符号和括号把数或表示数的字母连接而成的式子叫做代数式.单独的一个数或者一个字母也是代数式.加减乘除乘方注意：代数式肯定不含“=”、“>”、“<”例2上述代数式中，哪些是单项式，哪些是多项式．102r221x35xxx3335xy单项式单项式单项式多项式多项式→由数与字母的积或字母与字母的积所组成的代数式叫做单项式．单独一个数或字母也是单项式．→由几个单项式的和组成的代数式叫做多项式．单项式、多项式统称为整式．【注意：整式的分母肯定不含未知数！】例3.填空：（1）单项式的系数是，次数是．32xy124（2）单项式的系数是，次数是．322ab83→单项式中数字因数叫做这个单项式的系数．→一个单项式中，所有字母的指数的和叫做这个单项式的次数．例3填空．（3）多项式，是次项式，叫做，二次项系数是，叫做．3124235xxyx三四312x三次项常数项2345→多项式中的每个单项式叫做多项式的项．（注意：多项式中的每一项都包括它前面的符号！）→不含字母的项叫做常数项．→次数最高项的次数就是这个多项式的次数．例4.（1）选择题：下列说法中，正确的个数有……………………（）123①与是同类项5②与是同类项1aa③与是同类项23ab23ba④与是同类项2am2bm(A)1个(B)2个(C)3个(D)4个（2）如果与是同类项，那么m=_______，n=________.1213mnab212mab→所含字母相同，并且相同字母的指数也相同的单项式叫做同类项.→几个常数项也是同类项.√√××B21巩固练习1、下列说法正确的是（）.（A）一个代数式只有一个值.（B）代数式中的字母可以取任意的数值.（C）一个代数式的值与代数式中字母所取的值无关.（D）一个代数式的值由代数式中字母所取的值确定.D3xx巩固练习2、下列代数式中，单项式有（）.（A）1个.（B）2个.（C）3个.（D）4个.C03a41a)1(3122cba)(622yx36xyabx单项式多项式多项式多项式多项式多项式单项式单项式π是一个数.；；；；；；；巩固练习3、一个五次多项式，它任何一项的次数（）.（A）都小于5.（B）都等于5.（C）都不小于5.（D）都不大于5.D列代数式【先读先写！】（1）a，b的积除以a，b的差.（2）x减去1的差除以4所得的商.（3）x的减去y的3倍的差.（4）a与b两数的平方差.（5）a与b两数的差的平方.14abab134xy22ab2()ab（6）a与b的平方的差.2ab14x求代数式的值3a131323aaa4,3,2cbaacb4209332xyx2232yxyx（1）当时，求的值.时，计算代数式的值.，求代数式的值.（2）当（3）如果802332xy32按要求对多项式进行排列（1）把多项式按x的降幂排列.（2）先把按字母x降幂排列，再按字母y的升幂排列.yxxxyy232343222335yxyxyx32323223234342yxyxxyxxyxyy322332323322555xxxxyxyyxxyyyyyxyx（按字母x降幂排列）（按字母y升幂排列）如图，将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续去，……，根据以上操作方法，请你填写下表：操作次数N12345…100n…正方形个数47……1013163013n+1常见图形的周长和面积ababhbabakcbanmhacdbhhrrrLn)C=2(a+b)aaaaC=4aC=2(a+b)C=a+b+cC=a+b+c+dC=2πrC=2r+LS=abS=a2S=ah=bkS=ah=bn=cm1212121()2Sabh2Sr180nrL2360nSr;12SLr