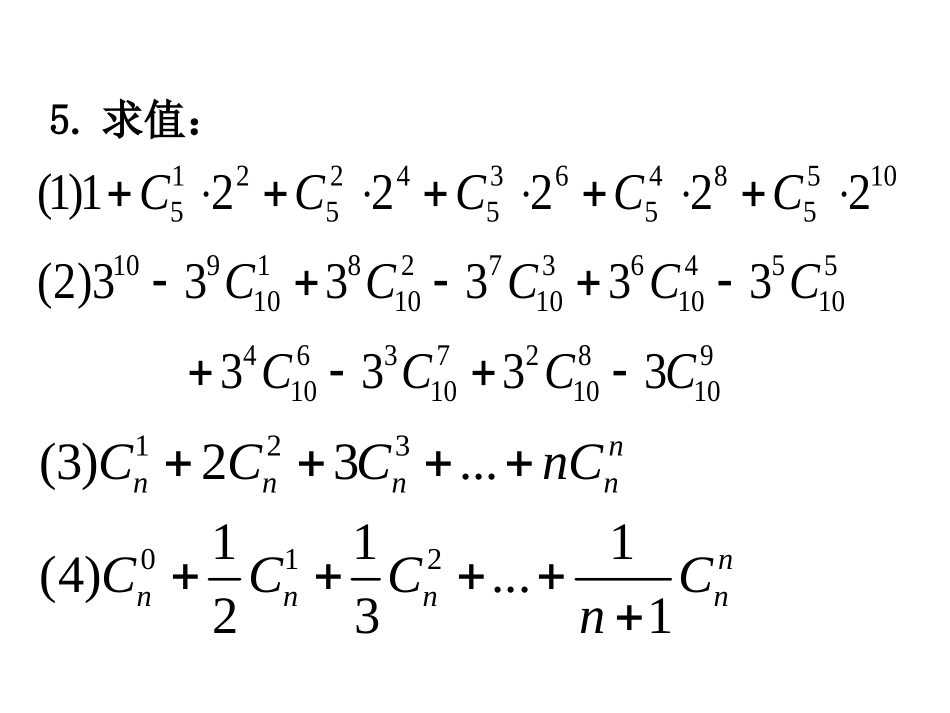【数学】131《二项式定理习题课》课件（新人教A版选修2-3）VIP免费

二项式定理习题课课堂练习：1.等于（）A.B.C.D.nnnnnnCCCC1321242n313n213n123n2．在的展开式中x的系数为（）A．160B．240C．360D．8005223xx3.求的展开式中项的系数.162)1()1()1(xxx3x4．已知那么的展开式中含项的系数是.2201212(1)(1)(1),nnnxxxaaxaxaxaa1na),1,(29nNnn6)1(yny5105410631072108110910333333)2(CCCCC1055845635425215222221)1(CCCCC9108102710361043333CCCC5.求值：123012(3)23...111(4)...231nnnnnnnnnnCCCnCCCCCn4234012342137(23),()xaaxaxaxaxaa2024、若则(a+a+a)的值为（）A.1B.-1C.0D.22360123601266...,...aaxaxaxaxaaaa6、（1-2x）则的值为（）A.1B.64C.243D.7293994x9ax、已知(-)的展开式中的系数为，x2常数的值为*8()nNn3n21、(2x+)的展开式中，若存在x常数项，则的最小值是（）A.3B.5C.8D.10725436167777345277103333,3331,ACCCBCCCAB7、设则的值为（）A.128B.129C.4D.011.证明(Cn0)2+(Cn1)2+(Cn2)2+…+(Cnn)2＝2)!()!2(nn12、将4个编号的球随机地放入3个编号的盒中，对每一个盒来说，所放的球数k满足。假定各种放法是等可能的，试求：⑴“第一盒中没有球”的概率；⑵“第一盒中恰有一球”的概率；⑶“第一盒中恰有两球”的概率；⑷“第一盒中恰有三球”的概率。04k44216813PA1344232813CPB2244224813CPC34428813CPD如何产生［a,b］区间上均匀随机数呢？利用计算器或计算机产生[0，1]上的均匀随机数x=RAND,然后利用伸缩和变换，就可得到[a,b]内的均匀随机数，试验的结果是[a,b]上的任何一个实数，并且任何一个实数都是等可能的。aabxx)(*1若(1)产生［0,100］区间上均匀随机数呢？(2)产生［100,150］区间上均匀随机数呢？练习、根据1.1.2例3中的程序框图，编写计算机程序来计算1+2+…+100的值i<=100?i=1开始输出s结束否是s=0i=i+1s=s+i程序：i=1s=0WHILEi<=100s=s+ii=i+1WENDPRINTsEND思考：用UNTIL语句编写计算机程序，来计算1+2+…+100的值.i=1开始结束s=0输出si=i+1s=s+ii>100?否是程序框图：程序：i=1s=0DOs=s+ii=i+1LOOPUNTILi>100PRINTsEND