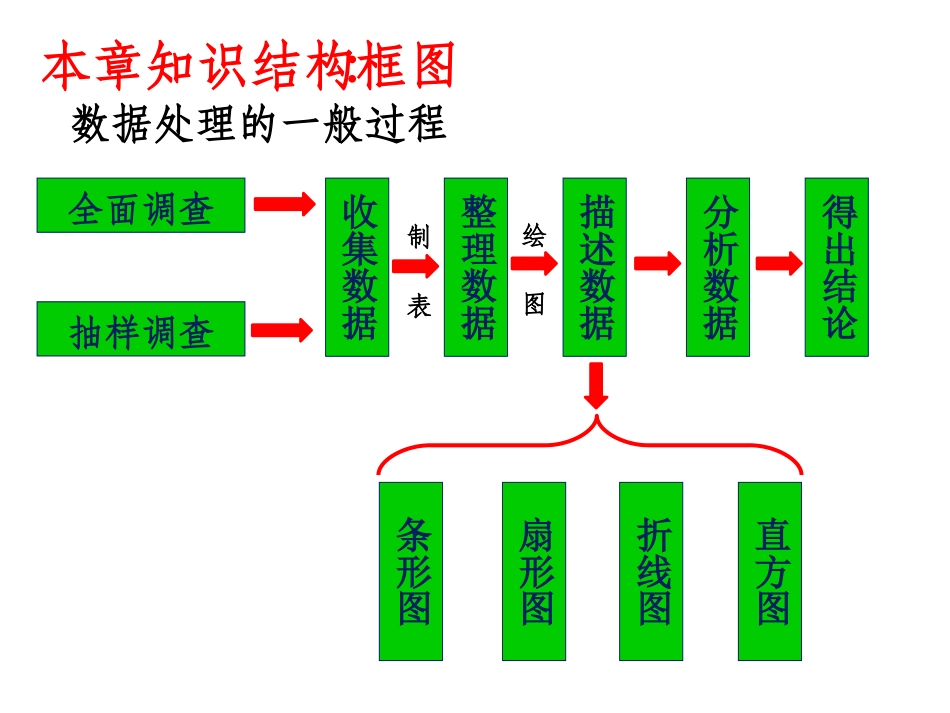
复习目标:1.根据情况区分运用全面调查和抽样调查。2.抽样调查中理解总体、样本、样本容量。3.根据直方图、扇形统计图、条形统计图、折线统计图获取数据,从而解决实际问题。绘图制表本章知识结构框图:数据处理的一般过程全面调查收集数据抽样调查得出结论分析数据整理数据描述数据直方图折线图扇形图条形图1.条形图能够显示每组中的__具体数量__,易于比较数据之间的__大小__.2.扇形图用扇形的大小表示__各个部分__所占百分比,易于显示每组数据相对于__总体__的大小,而不能判断出每组数据的__实际__大小.扇形圆心角的度数=__360°×百分比__.3.考察__全体对象__的调查叫做全面调查.1.对一组数据分组后,落在每个小组中的数据的个数叫__频数__;__频数与组距__的比值叫频率.2.画频数分布直方图的一般步骤:(1)计算最大值与最小值的差;(2)__决定组距和组数__;(3)__列频数分布表__;(4)画频数分布直方图.1.调查方式除全面调查外,还有__抽样__调查,简称__抽查__,它只抽取__一部分__对象进行调查,然后根据调查的数据推断__全体__对象的情况.2.在抽样调查中,要考察的全体对象称为__总体__,组成总体的每一个考察对象称为__个体__,被抽取的那些个体组成一个__样本__,一个样本中个体的__数目__称为样本容量.3.__全面调查和抽样调查__是收集数据的两种方式,全面调查收集到的数据__全面、准确__,但一般__花费多,耗时长__,而且某些调查不宜全面调查;抽样调查具有__花费少,省时__的特点,但抽取的样本是否具有__代表性__直接关系到对总体估计的__准确程度__.4.__用样本估计总体__是统计的基本思想.CBABD8827DAC0.3,60,20012BCBBBD21.(10分)某校七年级(1)班同学在“你我同心,抗击传染病”的募捐活动中,自愿捐款情况如下表.根据表格所给条件,回答下列问题:(1)该班共有___名学生;(2)该班共捐款___元;(3)根据上表信息制成条形统计图每人捐款数(元)251020相应的人数5102015解:如图22.(12分)小明参加卖报纸的实践活动,他调查了一个报亭某天A,B,C三种报纸的销售量,并把调查结果绘制成如下图所示的条形统计图.(1)求出该天A,C报纸的销售量各占这三种报纸销售之和的百分比;(2)请绘制该天A,B,C三种报纸销售量的扇形统计图;(3)小明准备按上述比例购进这三种报纸共100份,他应购进这三种报纸各多少份解:(1)4646+115+69×100%=20%,6946+115+39×100%=30%(2)图略(3)购A报纸:100×20%=20(份),购B报纸:100×50%=50(份),购C报纸:100×30%=30(份)23.(14分)在暑假社会实践活动中,小明所在小组的同学与一家玩具生产厂家联系,给该厂组装玩具,该厂同意他们组装240套玩具.这些玩具分为A,B,C三种型号,它们的数量比例以及每人每小时组装各种型号玩具的数量如图所示.若每人组装同一种型号玩具的速度都相同,根据以上信息,完成下列填空:(1)从上述统计图可知,A型玩具有____套,B型玩具有____套,C型玩具有____套.(2)若每人组装A型玩具16套与组装C型玩具12套所花的时间相同,求a的值并且求每人每小时组装C型玩具多少套?解:(1)240×55%=132240-132-60=48240×25%=60(2)168=122a-2,解得a=4,2a-2=2×4-2=625.(10分)(2014·兰州)兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机调查,并绘制出频数颁布表(如图1)和频数分布直方图(如图2)的一部分.(1)被调查的有多少名学生?(1)组距是多少?组数是多少?;(2)补全频数颁布直方图;(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业。时间(小时)频数(人数)频率0≤t<0.540.10.5≤t<1a0.31≤t<1.5100.251.5≤t<28b2≤t<2.560.15合计1