回归分析的基本思想及其初步应用课件VIP免费

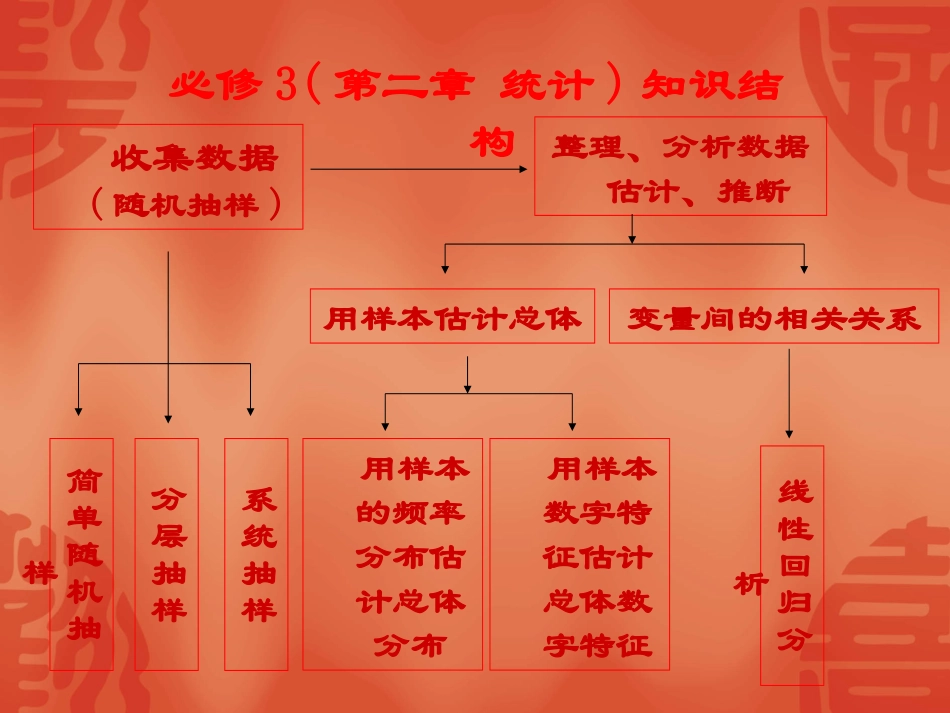
3.1回归分析的基本思想及其初步应用教学目标通过典型案例，掌握回归分析的基本思想及其初步应用。教学重点：熟练掌握回归分析的步骤。教学难点：求回归系数a,b及残差分析必修3(第二章统计)知识结构收集数据(随机抽样)整理、分析数据估计、推断简单随机抽样分层抽样系统抽样用样本估计总体变量间的相关关系用样本的频率分布估计总体分布用样本数字特征估计总体数字特征线性回归分析1、两个变量的关系不相关相关关系函数关系线性相关非线性相关问题1：现实生活中两个变量间的关系有哪些呢？相关关系：对于两个变量，当自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系。思考：相关关系与函数关系有怎样的不同？函数关系中的两个变量间是一种确定性关系相关关系是一种非确定性关系函数关系是一种理想的关系模型相关关系在现实生活中大量存在，是更一般的情况问题2：对于线性相关的两个变量用什么方法来刻划之间的关系呢？最小二乘估计最小二乘估计下的线性回归方程：ˆˆˆybxa121()()ˆ()niiiniixXyYbXXˆˆaYbX3、回归分析的基本步骤:画散点图求回归直线方程利用回归直线方程进行预报:,,,,,,,2211二乘估计公式分别为截距和斜率的最小我们知道其回归方程的关系的数据对于一组具有线性相关探究nnyxyxyx1xbˆyaˆ2,xxyyxxbˆn1i2in1iii?.y,x.yy,xn1xn1iin1ii公式吗你能推导出这两个计算称为其中样本点的中心.心回归直线过样本点的中.β,ααxβyβ,αQbˆaˆ,n1i2ii的值取最小值时分别是使和斜率截距从已经学过的知识知道n1i2iiαxβyxβyxβyβ,αQ由于2n1iii2iiαxβyαxβyxβyxβy2xβyxβy,αxβynαxβyxβyxβy2xβyxβy2n1iiin1i2iiαxβyxβyxβyn1iii注意到n1iiixβyxβyαxβyn1in1iiixβynxβyαxβy,0xβynxβnynαxβy2n1i2iiαxβynxβyxβyβ,αQ所以2n1i2iin1in1ii2i2αxβynyyyyxxβ2xxβ2n1i2in1iiin1i2i2xxyyxxβxxαxβyn.yyxxyyxxn1i2in1i2i2n1iii即有均为当且仅当前两项的值取最小值因此要使数而前两项为非负无关后两项和在上式中,0,Q,,β,α,.xβyα,xxyyxxβn1i2in1iii.公式这正是我们所要推导的.,基本思想及其应用进一步学习回归分析的下面我们通过案例.11,81所示重数据如表其身高和体名女大学生从某大学中随机选取例5943616454505748kg/170155165175170157165165cm/87654321体重身高编号.cm172,的女大学生的体重并预报一名身高为归方程身高预报她的体重的回求根据一名女大学生的:)11.1(.,,图图作散点体重为因变量真实取身高为自变量因此选据身高预报体重由于问题中要求根解yx4045505560657015015516016517017518011.1图xy.,,,11.1画它们之间的关系刻性回归方程以用线因此可线性相关关系较好的重有比高和体身样本点呈条状分布中可以看出从图.712.85xˆ849.0yˆ.849.0bˆ,712.85aˆ,21于是得到回归方程可以得到和根据探究中的公式.kg316.60712.85172849.0y,cm172,预报其体重为由回归方程可以的女大学生对身高为所以4045505560657015015516016517017518011.1图xy?.,849.0y,1x,849.0b的强弱它们之间线性相关关系如何描述性相关关系体重与身高具有正的线这表明个单位就增加体重个单位时每增加说明身高是斜率的估计值为关系数的具体计算公式样本相关系的方法两个变量之间线性相关来衡量我们介绍...