结识抛物线任慧VIP免费

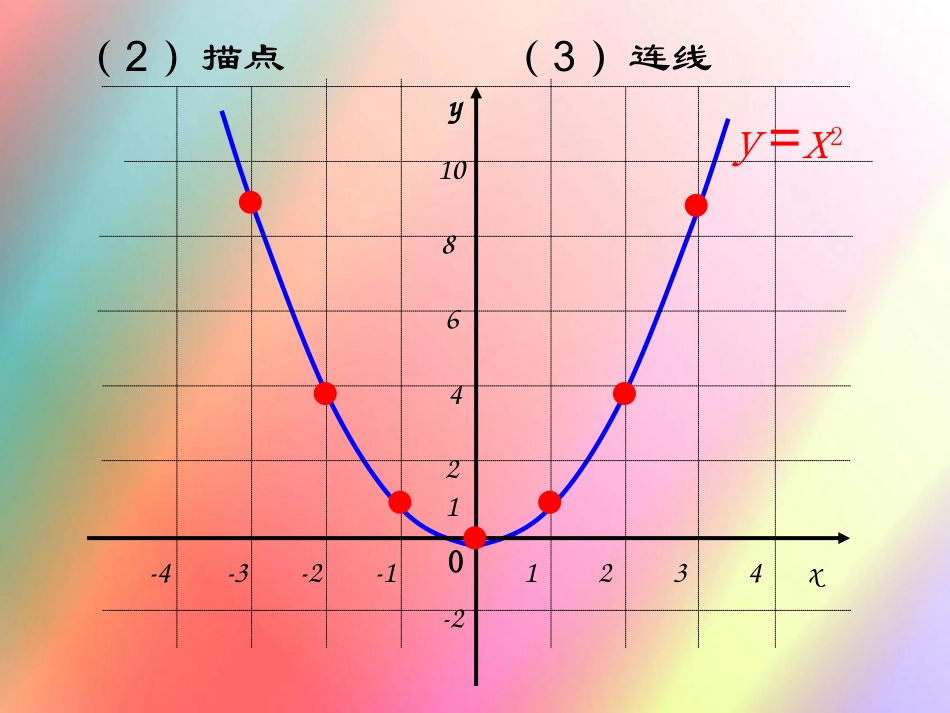
二次函数y=x2的图象(1)列表xy=x2-39-24-110011439……2222……作出xy0-4-3-2-11234108642-21y=x2（2）描点（3）连线01234-1-2-3-42468XY1001234-1-2-3-42468XY1001234-1-2-3-42468XY10(1)(3)(2)01234-1-2-3-42468Xy10(4)2xy二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.o创设情景引入新课开封清明上河园虹桥北京颐和园十七孔桥绚丽的天边彩虹灿烂的夜光喷泉水中欢跳的海豚空中绽放的烟花这条抛物线关于y轴对称,y轴就是它的对称轴.2xy交流协作回答问题(1)图象是轴对称图形吗？如果是,它的对称轴是什么?(2)图象与x轴有交点吗？如果有,交点坐标是什么?(4)随着x值的变化,y的值如何变化？图象与图象与x轴有交点，交点为(0,0)当x=0时，y最小=0最小?最小值是什么？(3)当x取什么值时,y的值对称轴与抛物线的交点叫做抛物线的顶点抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展；当x=0时,函数y的值最小，最小值是0。2xy当x<0(在对称轴的左侧)时,y随着x的增大而减小。当x>0(在对称轴的右侧)时,y随着x的增大而增大。①y=-x2②y=x2，③y=2x2，④y=-2x221请同学们画出下列几个函数的图象要求四人小组不重复的每人画一个函数图象。y=-x201234-1-2-3-4-2-4-6-8XY-10观察图象,回答问题y=-x201234-1-2-3-4-2-4-6-8XY-10(1)形状：抛物线(2)开口方向：向下(3)对称轴：y轴(4)顶点坐标：（0，０）(5)最值：(6)增减性：在对称轴的左侧,y随着x的增大而增大.（x<0）右侧,y随着x的增大而减小（x>0）当x=0时，y最大=0在同一坐标系中作出函数y=x2和y=-x2的图象.3.532.521.510.5-2-1122xy22xy221xyyx0Oxy221xy22xy2xy2xy22xy221xyyx03.532.521.510.5-2-112a＞0a＜02xyy22xyx0221xyy0x221xy221xy22xy22xy2xy2xyy0x221xy221xy22xy22xy2xy2xy(3)点A（），B（）在抛物线y=x2上，则ab2xya,21b,32231xy(1)抛物线在x轴的方(除顶点外),在对称轴的左侧,y随着x的增大而___(2)抛物线有最点，其坐标为____,对称轴为_____.下增大低（0，0）y轴﹤（4）抛物线y=4x2，y=0.25x2，y=–0.25x2的共同特点是（）A．关于y轴对称，开口向上B．关于y轴对称，y随x的增大而增大C．关于y轴对称，y随x的增大而减小D．关于y轴对称，顶点是原点（5）是关于x的二次函数，其图象与y=x2的图象关于对称。D322mmmxyx轴已知二次函数272xy①29.0xy②26.0xy⑤2133xy⑥23xy④215xy③（1）其中开口向下的有_________(2)其中有最大值的有________(3)当自变量由小到大变化时，函数值先逐渐变大，然后逐渐变小的有_______①④⑤①④⑤①④⑤已知三点（1，y1）（0.5，y2）（n，y3）都在函数y=x2的图象上且n1﹥，则（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y1＜y3D函数y=ax2(a>0)y=ax2(a<0)开口方向向上向下对称轴y轴y轴顶点坐标（0，0）（0，0）增减性当x<0时,y随着x的增大而减小.当x>0时,随着x的增大而增大.最值当x=0时,最小值为0.当x=0时,最大值为0.当x<0时,y随着x的增大而增大.当x>0时,随着x的增大而减小.函数y=ax2(a≠0)的图象和性质yxoyxo图象作业：知识与技能：第2题数学理解：第3题p44已知函数是关于x的二次函数,求：（1）满足条件的m的值；(2)当m=___时，抛物线有最低点，最低点的坐标为______，这时当x___时，y随x的增大而增大.(3)m=___时，函数有最大值，最大值是___,这时当x0﹤时，y随x的增大而____.42)2(mmxmy课外作业