平行线的证明强化训练1VIP免费

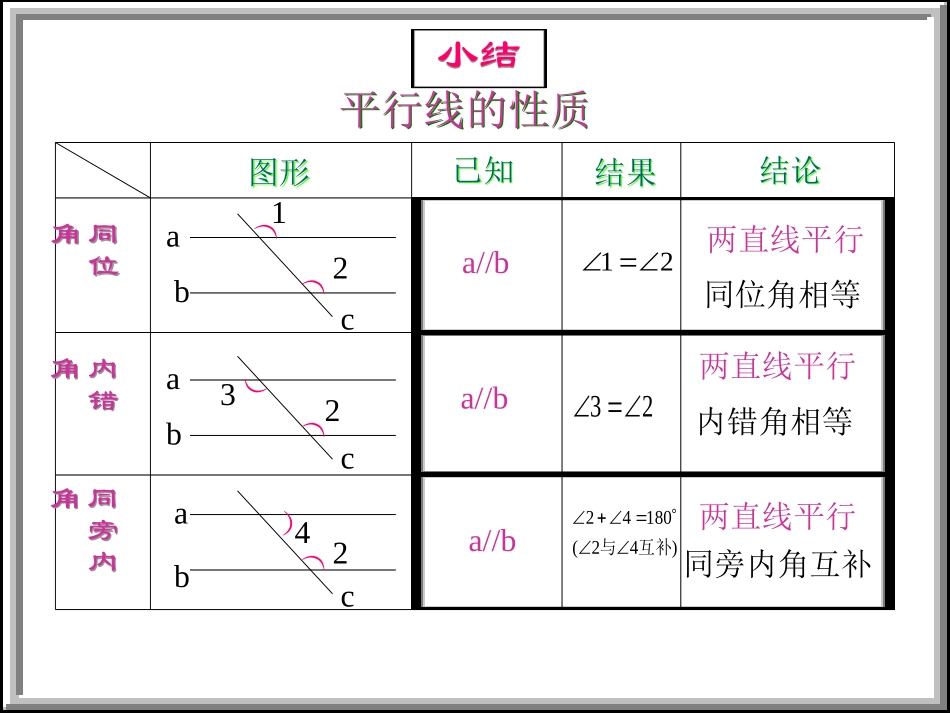
图形图形已知已知结果结果结论结论同位角同位角内错角内错角同旁内角同旁内角23)42(18042互补与a//ba//b内错角相等两直线平行同旁内角互补两直线平行122324））））））abababccc平行线的性质平行线的性质小结小结21a//b同位角相等两直线平行21a//b同位角相等两直线平行21a//b同位角相等两直线平行21a//b同位角相等两直线平行a//b21两直线平行同位角相等a//b23两直线平行内错角相等同旁内角互补a//b)42(18042互补与两直线平行同位角相等内错角相等同旁内角互补两直线平行两直线平行判定性质性质已知得到得到已知小结：复习回顾复习回顾新课学习新课学习巩固练习巩固练习课堂小结课堂小结如图，已知：∠1=2∠，∠1=B∠，求证：ABEF∥，DEBC∥。证明:∵1=2∠∠（已知），∴ABEF()∥又∵∠1=B∠（）.∴___∥___(同位角相等，两直线平行)FAEDCB12内错角相等，两直线平行已知DEBC如图，已知：∠1+2=180°∠，求证：ABCD.∥证明:∵∠1+∠2=180°(已知)，∠1=∠3（对顶角相等）.∴∠2=∠4（）∵∠3+=180°()∴____∥_____.()4123ABCEFD对顶角相等∠4ABCD等量代换同旁内角互补,两直线平行如图，已知：∠DAF=AFE∠，∠ADC+DCB=180°∠，求证：EFBC∥证明:∵DAF=AFE∠∠（）∴AD____()∥∵∠ADC+=180°（已知）.∴AD∥.()∴EFBC()∥ADBCFE已知内错角相等，两直线平行EF∠DCB同旁内角互补，两直线平行BC平行于同一直线的两条直线互相平行如图，已知：∠2=3∠，∠1+3=180°∠，求证：EFGH.∥证明：∵∠2=3∠（已知）∠1+3=180°∠（）∴∠1+2=180°()∠∴________.()∥231ABCDEFGH已知等量代换同旁内角互补，两直线平行EFGH如图，已知：∠1=2∠，BD平分∠ABC，试说明ADBC.∥证明：∵BD平分∠ABC（已知），∴∠2=3.()∠∵∠2=1∠（已知）∴∠3=_____()∴___∥.()DBAC123角平分线定义等量代换∠1ADBC内错角相等,两直线平行如图，已知：ABCD∥，AEBD∥，试说明∠ABD=E.∠证明：∵_________（已知），∴∠ABD=______()∵AEBD∥（）.∴∠BDC=E.()∠∴_______=_____()ABCEDAB∥CD∠BDC已知两直线平行，同位角相等∠ABDE∠两直线平行，同位角相等等量代换如图，已知：ACDE∥，∠1=2∠，试说明ABCD.∥证明：∵ACDE∥（已知），∴∠ACD=.()∵∠1=2∠（已知）.∴∠1=ACD.()∠∴___∥.()ADBE12C∠2等量代换内错角相等，两直线平行ABCD两直线平行,内错角相等1.如图，已知：ABCD∥，∠1=55°2=80°∠，求∠3的度数.123ABCEFD42.如图，已知：ABCD∥，∠A=70°DH∠E=70°,求证：AMEF∥FMEABCDHG1.如图１，ABCD,1=45°,D=C,∥∠∠∠依次求出∠Ｄ，∠Ｃ，∠Ｂ的度数．2.在下图所示的３个图中，ab∥，分别计算∠１的度数．DCAB1baaabb11136°120°