加减法解二元一次方程组VIP免费

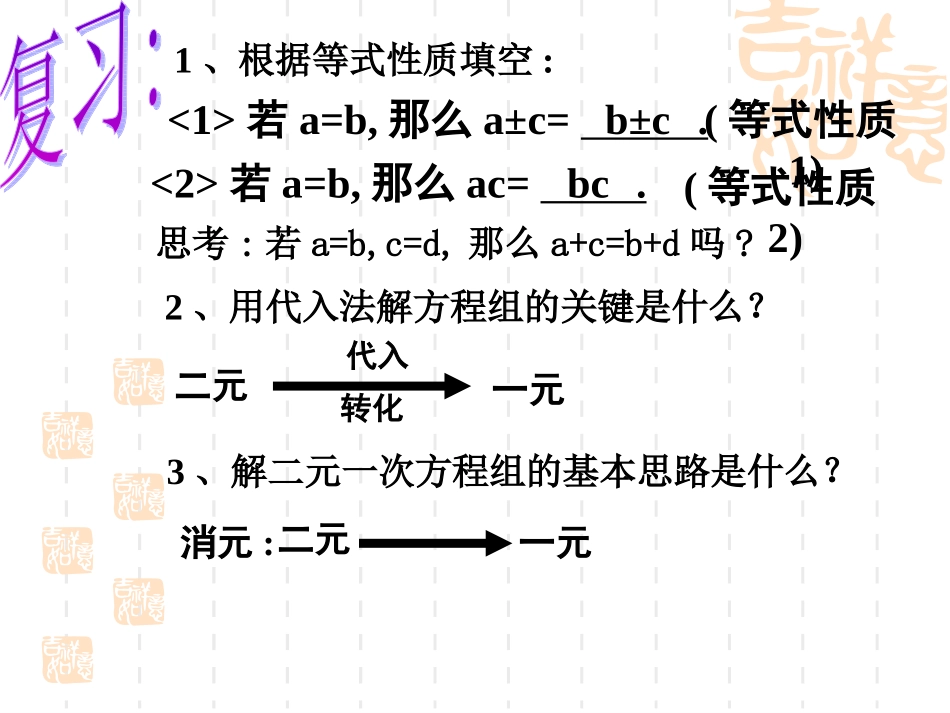
2、用代入法解方程组的关键是什么？1、根据等式性质填空:思考:若a=b,c=d,那么a+c=b+d吗?3、解二元一次方程组的基本思路是什么？b±cbc(等式性质1)(等式性质2)<2>若a=b,那么ac=.<1>若a=b,那么a±c=.一元代入转化二元消元:二元一元用代入法怎样解下面的二元一次方程组呢？40222yxyx①②还有别的方法吗？认真观察此方程组中各个未知数的系数有什么特点，并分组讨论看还有没有其它的解法.并尝试一下能否求出它的解40222yxyx①②2x-5y=7①2x+3y=-1②解方程组和y5y5互为相反数……352125-11xyxy①②加减消元法两个二元一次方程中同一未知数的系数相等或互为相反数时，将两个方程的两边分别相减或相加，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法，简称加减法.11522153-yxyx①②2x-5y=7①2x+3y=-1②分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x填空题：只要两边只要两边6x+7y=-196x-5y=173x+2y=133x-2y=5加减法解方程组：⑴⑵用加减法解方程组:分析：对于当方程组中两方程不具备上述特点时，则可用等式性质来改变方程组中方程的形式，即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组，从而为加减消元法解方程组创造条件．2x+y=3x+4y=5⑴⑵解方程组：3x+2y＝72x+5y＝1(1)2x+y＝33x－5y＝11(2)5x+2y＝33x+5y＝-2上面这些方程组的特点是什么?解这类方程组基本思路是什么？主要步骤有哪些？主要步骤：特点:基本思路:写解求解加减二元一元加减消元:消去一个元分别求出两个未知数的值写出原方程组的解同一个未知数的系数相同或互为相反数127xy解：由①×6，得2x+3y=4③由②×4，得2x-y=8④由③-④得:y=-1所以原方程组的解是把y=-1代入②，解得:27x②①24121231yxyx用加减消元法解方程组：通过本课的学习，你有什么收获？用加减法解下列方程组：3216,31;mnmn234,443;xyxy523,611;xyxy357,234232.35xyxy谢谢大家！