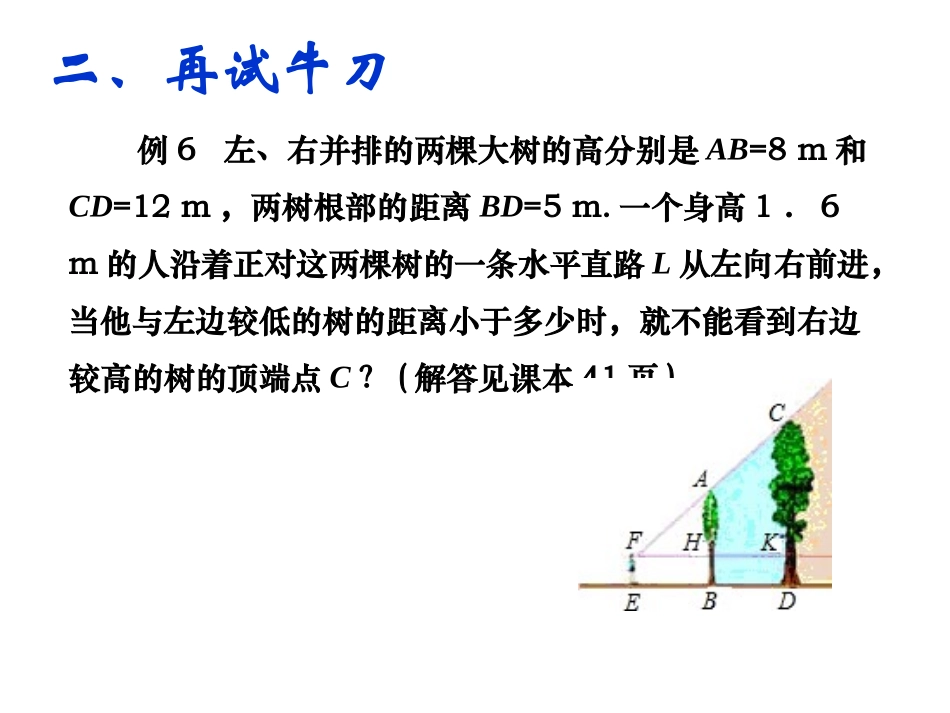
第二十七章相似27.2.227.2.2相似三角形应用举例相似三角形应用举例((22))一、新课引入利用相似可以解决生活中的问题,计量一些无法直接测量的物体的长度.解题的关键在于构建相似三角形.例6左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树根部的距离BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?(解答见课本41页)二、再试牛刀例3:已知左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。一个身高1.6m的人沿着正对着两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看见右边较高的树的顶端点C?KⅡ盲区观察者看不到的区域。仰角:视线在水平线以上的夹角。水平线视线视点观察者眼睛的位置。(1)FBCDHGlAK(1)FBCDHGlAⅠKFABCDHGKⅠⅡl(2)分析:假设观察者从左向右走到点E时,他的眼睛的位置点F与两颗树的顶端点A、C恰在一条直线上,如果观察者继续前进,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它。E由题意可知,ABL⊥,CDL⊥,∴ABCD∥,△AFHCFK∽△∴FHFK=AHCK即FHFH+5=8-1.612-1.6解得FH=8∴当他与左边的树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,就不能看见右边较高的树的顶端点C你能设计方案,利用相似三角形的知识测量旗杆的高度吗?方法一:利用阳光下的影子三、提出问题操作方法:一名学生在直立于旗杆影子的顶端处,测出该同学的影长和此时旗杆的影长.点拨:把太阳的光线看成是平行的. 太阳的光线是平行的,∴AE∥CB,∴∠AEB=∠CBD. 人与旗杆是垂直于地面的,∴∠ABE=∠CDB,∴△ABE∽△CBD.∴.即CD=.因此,只要测量出人的影长BE,旗杆的影长DB,再知道人的身高AB,就可以求出旗杆CD的高度了.BEBDABBDBECDAB方法二:利用镜子的反射操作方法:选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆项端.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.点拨:入射角=反射角 入射角=反射角,∴∠AEB=∠CED. 人、旗杆都垂直于地面,∴∠B=∠D=90°.∴.因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度.DEBECDAB方法三:利用标杆测量旗杆的高度操作方法:选一名学生为观测者,在他和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,分别测出他的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度.点拨:人、标杆和旗杆都垂直于地面. 人、标杆和旗杆都垂直于地面,∴∠ABF=∠EFD=∠CDH=90°,∴人、标杆和旗杆是互相平行的. EF∥CN,∴∠1=∠2. ∠3=∠3,△AME∽△ANC,∴. 人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,∴能求出CN. ∠ABF=∠CDF=∠AND=90°,∴四边形ABND为矩形.∴DN=AB.∴能求出旗杆CD的长度.CNEMANAM8.为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.hSACBB'OC'A'9、如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明得身高为1.6m,求路灯杆AB的高度。DFBCEGAPDQBCA10.10.如图,小华在晚上由路灯如图,小华在晚上由路灯AA走向路灯走向路灯BB,当他走,当他走到点到点PP时,发现他身后影子的顶部刚好接触到路灯时,发现他身后影子的顶部刚好接触到路灯AA的底部,当他向前再步行的底部,当他向前再步行12m12m到达点到达点QQ时,发现他时,发现他身前影子的顶部刚好接触到路灯身前影子的顶部刚好接触到路灯BB的底部,已知小华的底部,已知小华的身高是的身高是1.60m1.60m,...