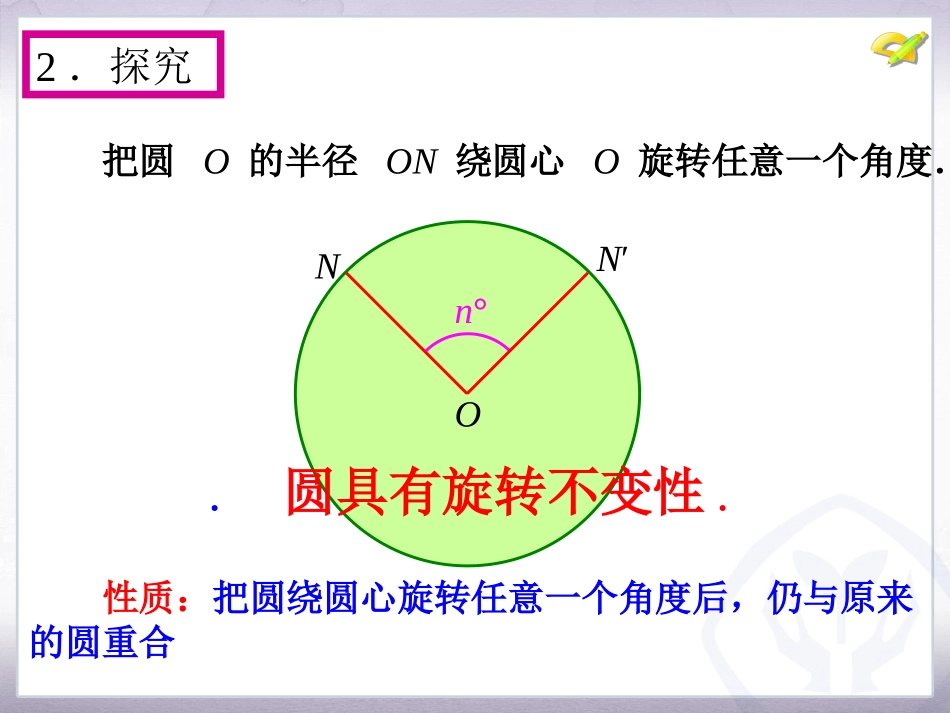
24.1圆的有关性质(第3课时)九年级上册1.探究圆是中心对称图形吗?它的对称中心在哪里?圆是中心对称图形,它的对称中心是圆心,把圆O的半径ON绕圆心O旋转任意一个角度.2.探究NOn°N′性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.圆具有旋转不变性.把圆O的半径ON绕圆心O旋转一个角度,得到∠NOM,它的顶点在哪里?2.认识圆心角M我们把顶点在圆心的角叫做圆心角.如∠NOM.NOn°3.探究如图,当圆心角∠AOB=∠COB‘时它们所对的弧有何关系?为什么?'ABOB'A'AB=''ABAB=AB''AB与''ABAB与AB''同样,还可以得到:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的弧______.这样,我们就得到下面的定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.相等相等相等相等4.定理同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.因为AB=CD,所以∠AOB=∠COD.又因为AO=CO,BO=DO,所以△AOB≌△COD.又因为OE、OF是AB与CD对应边上的高,所以OE=OF.5.巩固∠AOB=∠CODAB=CD如图,AB、CD是⊙O的两条弦:(1)如果AB=CD,那么________,______________;(2)如果=,那么________,______________;(3)如果∠AOB=∠COD,那么________,_______;(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?ABCDAB=CDAB=CD∠AOB=∠CODAB=CD相等.ABCDEFO∴AB=AC,△ABC等腰三角形.又∠ACB=60°,∴△ABC是等边三角形,AB=BC=CA.∴∠AOB=∠BOC=∠AOC.6.例题例1如图,在⊙O中,=,∠ACB=60°.求证:∠AOB=∠BOC=∠AOC.ABAC证明:ABAC∵=ABCO1、如图,AB是⊙O的直径,==,∠COD=35°,求∠AOE的度数.·AOBCDE解:CDBCDE∴∠BOC=∠COD=∠DOE=35°∴∠AOE=180°-3×35°=75°CDBCDE==∵6.练习2、如图,在⊙O中,AB和CD是直径。求证:(1)四边形ABCD为矩(2)圆心角∠AOB为多少度时,四边形ABCD为正方形为什么?ABO6.练习DC解:(1)∵∠BOC=∠AOD,∠AOB=∠DOC∴AD=BCAB=CD∴四边形ABCD为平行四边形又∵AC=BD∴平行四边形ABCD为矩形(2)当∠AOB=90°时,四边形ABCD为正方形。∴∠AOB=∠BOC=90°∵∠AOB=90°∴AB=BC∴矩形ABCD为正方形。(1)本节课学习了哪些内容?(2)圆心角、弧、弦之间有哪些关系?7.课堂小结教科书习题24.1第3,4题.8.布置作业