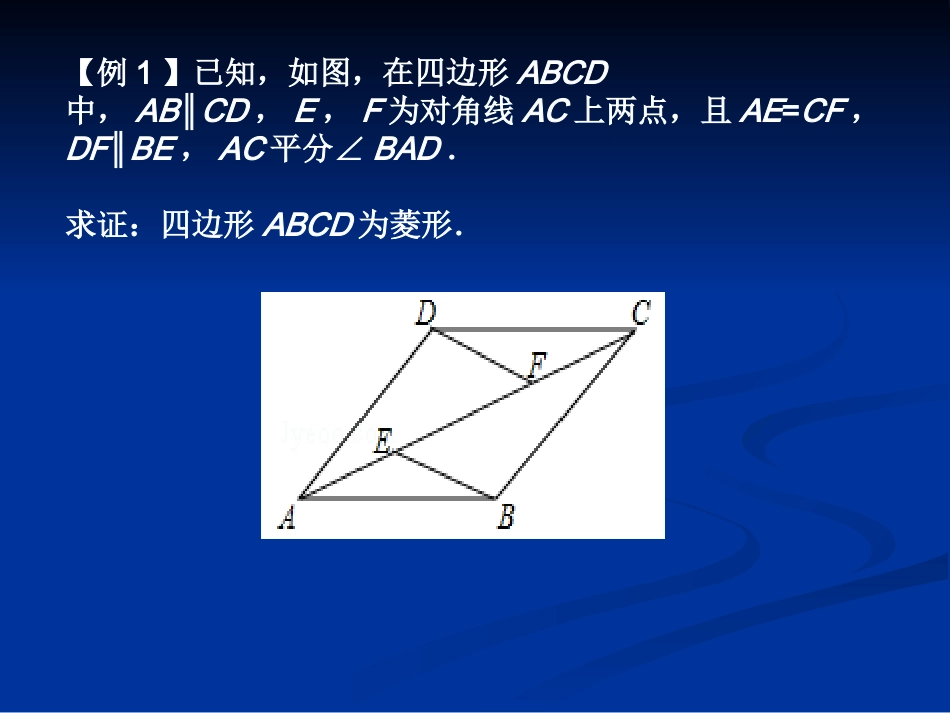
三角形、四边形的证明与计算石河子第三中学刘亚南考点、热点分析1.了解多边形的内角和与外角和公式,掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系.了解四边形的不稳定性;2.掌握平行四边形对边相等、对角相等、对角线互相平分的性质,四边形是平行四边形的条件(一组对边平行且相等,或两组对边分别相等,或对角线互相平分的四边形是平行四边形);了解中心对称图形及其基本性质;3.掌握矩形、菱形、正方形的有关性质和四边形是矩形、菱形、正方形的条件;4.了解等腰梯形同一底上的两底角相等,两条对角线相等的性质,以及同一底上的两底角相等的梯形是等腰梯形的结论5.进一步认识三角形的有关概念,了解三边之间的关系以及三角形的内角和,了解三角形的稳定性。6.了解图形的全等,能利用全等图形进行简单的图案设计。7.经历探索三角形全等条件的过程,掌握两个三角形全等的条件,能应用三角形的全等解决一些实际问题。8.在分别给出两角夹边、两边夹角和三边的条件下,能够利用尺规作出三角形(会写已知、求作和作法,不要求证明)。【例1】已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.∵AB=CD,BC=AD∴四边形ABCD是平行四边形∴AB∥CD∴∠BAE=∠DCF又∵AE=CF∴△ABE≌△CDF(SAS)∴AB=CD,∵AB∥CD∴四边形ABCD是平行四边形∴AD=CD∵AC平分∠BAD∴∠BAE=∠DAF∵∠BAE=∠DCF∴∠DAF=∠DCF∴四边形ABCD是菱形.【例2】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)(1)作∠DAC的平分线AM;(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明:判断四边形AECF的形状并加以证明.DCBA①如图所示②证明:∵AB=AC,AM平分∠CAD∴∠B=ACB∠,∠CAD=2CAM∠∵∠CAD是△ABC的外角∴∠CAD=B+ACB∠∠∴∠CAD=2ACB∠∴∠CAM=ACB∠∴AFCE∥∵EF垂直平分AC∴∠FAO=ECO,OA=OC,∠∠AOF=COE∠,∴AOFCOE≌△∴AF=CE在四边形AECF中,AFCE∥,AF=CE∴四边形AECF是平行四边形又∵EFAC⊥∴四边形AECF是菱形【例3】已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AEBC∥,CE⊥AE;垂足为E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.【例4】在四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.(1)如图①,试判断四边形EGFH的形状,并说明理由;(2)如图②,当EF⊥GH时,四边形EGFH的形状是;(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是;(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.(1)四边形EGFH是平行四边形.证明:∵ABCD的对角线AC、BD交于点O.∴点O是ABCD的对称中心.∴EO=FO,GO=HO.∴四边形EGFH是平行四边形(2)菱形(3)菱形(4)四边形EGFH是正方形.∵AC=BD,∴ABCD是矩形.又∵AC⊥BD,∴ABCD是菱形.∴ABCD是正方形,∴∠BOC=90°∠GBO=∠FCO=45°OB=OC.∵EF⊥GH,∴∠GOF=90°.∴∠BOG=∠COF.∴△BOG≌△COF.∴OG=OF,∴GH=EF.由(1)知四边形EGFH是平行四边形又∵EF⊥GH,EF=GH.∴四边形EGFH是正方形.【例5】如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.(1)如果①:求证∠AFD=EBC∠;(2)如图②,若DE=EC且BEAF⊥,求∠DAB的度数;(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)(1)证明:∵四边形ABCD为菱形,∴DC=CB,在△DCE和△BCE中,DC=CBDCE∠=∠BCEEC=EC,∴△DCEBCE≌△(SAS),∴∠EDC=EBC∠,∵DCAB∥,∴∠EDC=AFD∠,∴∠AFD=EBC∠;(2)解:∵DE=EC,∴∠EDC=ECD∠,设∠EDC=ECD=CBE=x°∠∠,则∠CBF=2x°,由BEAF⊥得:2x+x=90°,解得:x=30°,∴∠DAB=60°;DCBAEF(3)∵∠EFB为钝角,∴只能是FE=FB,设∠BEF=EBF=x°∠,则有∠AFD=2x°,可证得:∠AFD=FDC=CBE∠∠,得x+2x=90,解得:x=30,∴∠EFB=120°,综上:∠EFB=30°或120°.BDCAEF课堂小结•知识在线:加深了对考点的认识;熟悉了解决问题的常用方法•思想方法:分类讨论;转化思想