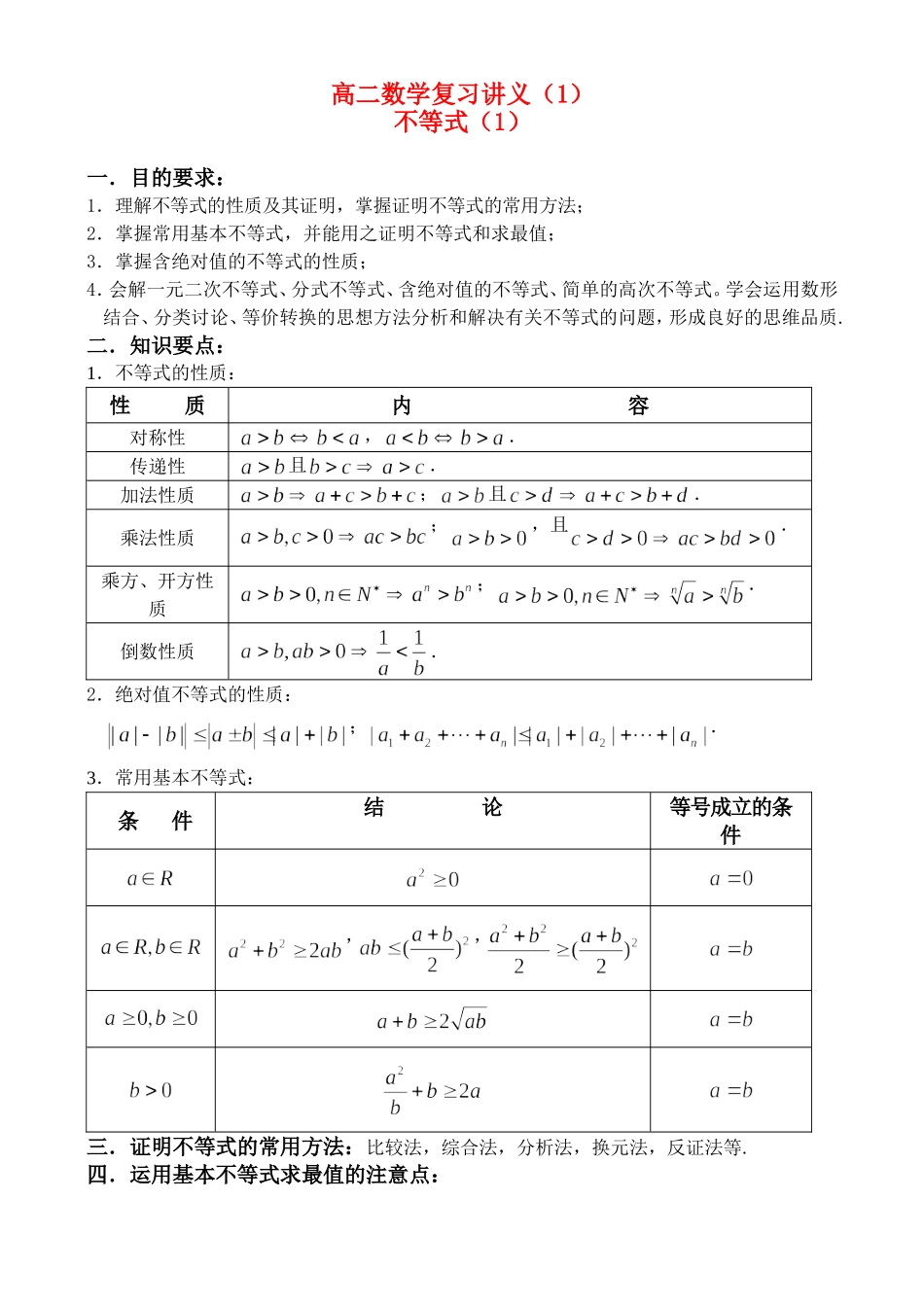
高二数学复习讲义(1)不等式(1)一.目的要求:1.理解不等式的性质及其证明,掌握证明不等式的常用方法;2.掌握常用基本不等式,并能用之证明不等式和求最值;3.掌握含绝对值的不等式的性质;4.会解一元二次不等式、分式不等式、含绝对值的不等式、简单的高次不等式。学会运用数形结合、分类讨论、等价转换的思想方法分析和解决有关不等式的问题,形成良好的思维品质.二.知识要点:1.不等式的性质:性质内容对称性,.传递性且.加法性质;且.乘法性质;,且.乘方、开方性质;.倒数性质.2.绝对值不等式的性质:;.3.常用基本不等式:条件结论等号成立的条件,,三.证明不等式的常用方法:比较法,综合法,分析法,换元法,反证法等.四.运用基本不等式求最值的注意点:①常用的不等式:,,.②注意点:和定积最大,积定和最小;一正、二定、三相等.五.常见不等式及其基本解法:1.一元二次不等式:(1)利用其与一元二次方程,二次函数的关系;(2)含字母系数的一元二次不等式大致分为两类:①的符号不确定,讨论的大小;②通过因式分解(或求根公式)得出两根,但根的大小不明确,则讨论根的大小.(3)一元二次不等式的应用:①已知一个不等式的解集,求另一个不等式的解集;②恒成立问题:通常可结合二次函数图象来考虑.2.分式不等式:移项,通分,再转化为不等式组或序轴标根;3.含有绝对值的不等式:用绝对值的定义去掉绝对值符号.4.高次不等式:序轴标根法;5.指数、对数不等式:利用指数函数、对数函数的单调性进行等价转化.六.例题分析:例1.已知,,,求证:.证明:∵,∴,又,∴,∴,又,∴.例2.已知都是实数,求证:,并指出何时成立.比较法或综合法,成立的条件是.例3.已知,,求证:.证明:∵,∴,又,∴,∴,要证,只要证,只要证,即,只要证,∵,∴只要证,即,∵成立,∴.例4.在中,为三条边的长,表示的面积,求证:,并说明“”成立的条件.证明:由余弦定理,有,又,∴,∵,∴,∴,当且仅当,即,也就是是等边三角形时,“”成立.七.课后作业:班级学号姓名1.已知,则下列不等式一定成立的是()2.下列命题中成立的是(),当且仅当时成立;,当且仅当时成立;,当且仅当时成立;,当且仅当时成立。3.若,且,则下列结论中成立的是()异号,;异号,;同号,;同号,.4.已知两实数的算术平均数为,实数,,,则与的大小关系为.5.函数的最大值为,此时的值为.6.已知,求证.7.在中,三条边的长成等差数列,求角的取值范围.8.已知都是实数,求证:.9.若,求证:.10.已知实数满足不等式,求证:.