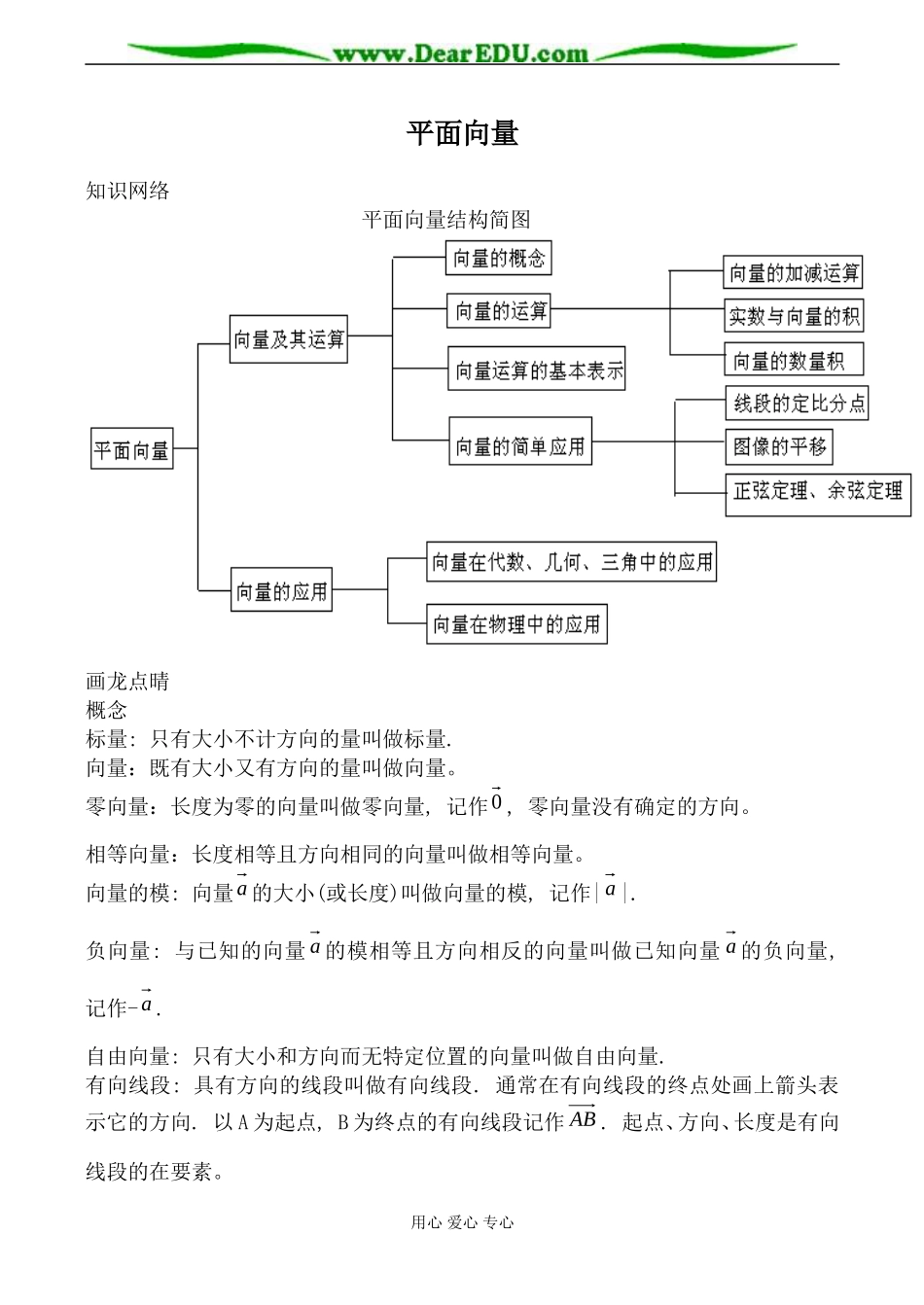
平面向量知识网络平面向量结构简图画龙点晴概念标量:只有大小不计方向的量叫做标量.向量:既有大小又有方向的量叫做向量。零向量:长度为零的向量叫做零向量,记作0,零向量没有确定的方向。相等向量:长度相等且方向相同的向量叫做相等向量。向量的模:向量a的大小(或长度)叫做向量的模,记作|a|.负向量:与已知的向量a的模相等且方向相反的向量叫做已知向量a的负向量,记作-a.自由向量:只有大小和方向而无特定位置的向量叫做自由向量.有向线段:具有方向的线段叫做有向线段.通常在有向线段的终点处画上箭头表示它的方向.以A为起点,B为终点的有向线段记作AB.起点、方向、长度是有向线段的在要素。用心爱心专心用有向线段表示向量:已知向量a与有向线段AB.当|a|=|AB|且a与AB同向时,向量a可用有向线段AB表示,叫做向量AB.向量加法:求两个向量的和的运算,叫做向量的加法。向量加法的平行四边形:平面上任意两个向量a、b,从同一点O出发分别作向量OA=a,OB=b,以OA、OB为一组邻边作平行四边形OACB,则平行四边形的对角线OC所代表的向量OBOAOC=a+b。向量加法的三角形法则:平面上任意两个向量a、b,任取一个起点O,从O出发作向量OA=a,再从A出发作向量AB=b,则OB=OA+AB=a+b。说明:(1)“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点;(2)可以推广到n个向量连加,和向量就是以第一个向量的起点为起点,最后一个向量的终点为终点的向量;(3)aaa00;(4)不共线向量都可以采用这种法则——三角形法则.向量的加法运算律:(1)交换律:a+b=b+a;(2)向量加法的结合律:(a+b)+c=a+(b+c).向量的减法:平面上任意两个向量a、b,从同一点O出发分别作向量OA=a,OB用心爱心专心=b,作向量BA,则向量BA叫做向量a与b的差,记作a-b,即BA=a-b.[活用实例][例1]试用向量方法证明:对角线互相平分的四边形是平行四边形。[题解]由向量加法法则:AB=AO+OB,DC=DO+OC由已知:AO=OC,DO=OB∴AB=DC,即AB与CD平行且相等∴ABCD为平行四边形.[例2]在正六边形中,若OA=a,OE=b,试用向量a、b将OB、OC、OD表示出来。[题解]设正六边形中心为P,则OAOEOAPBOPOB)(a+b+aPCOPOCa+b+a+b由对称性:OD=b+b+a。[例3]设A、B、C、D、O是平面上的任意五点,试化简:(1)CDBCAB;(2)BDACDB;(3)COOBOCOA.[题解](1)原式=ADCDACCDBCAB)(;(2)原式=ACACACBDDB0)(;用心爱心专心ABDCOABOPCEF(3)原式=ABABCOOCABCOOCOAOB0)()()(.实数与向量的积:一般地,实数λ与向量a的积是一个向量,记作λa;它的长度与方向规定如下:(1)|λa|=|λ||a|;(2)当λ〉0时,λa的方向与a的方向相同;当λ〈0时,λa的方向与a的方向相反;当λ=0时,λa=0,并且满足|λa|=|λ||a|.其中实数λ叫做a的系数.实数与向量的积的运算定律:结合律:λ(μa)=(λμ)a;第一分配律:(λ+μ)a=λa+μa;第二分配律:λ(a+b)=λa+λb.平行向量:当两个非零向量的方向相同或相反时,称这两个向量是平行向量,也称共线向量.单位向量:长度等于1个单位长度的向量叫做单位向量.向量a的大小由|a|表示而它的方向可由||aa表示.向量b与非零向量a共线的充要条件是:有且只有一个非零实数λ,使b=λa.[活用实例][例4]O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足),,0[),||||(ACACABABOAOP则P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心[题解]||||ACACABAB、分别表示直线AB、AC上的单位向量,它们的和向量||||ACACABAB平分BAC,所以原题转化为),0[),||||(当ACACABABAP时,它表示以A为顶点,终点P在BAC上的所有向量,所以点P的轨迹过ABC的内心.故选B.[例5]如图:已知MN是△ABC的中位线,求证:MN=21BC,且MN∥BC.用心爱心专心ABCNM[题解] MN是△ABC的中位线,∴ABAM21,ACAN21∴BCABACABACAMANMN21)(212121∴MN=21BC,且MN∥BC.[例6]设非零向量a、b不共线,c=ka+b,d=a+kb(kR),若c∥d,试求k.[题解] c∥d∴由向量共线的充要条件得:c=λd(λR)即:ka+b=λ(a+kb)∴(k...