高中数学：3.1.1 两角和与差的余弦 二 教案 新人教B版必修4VIP免费

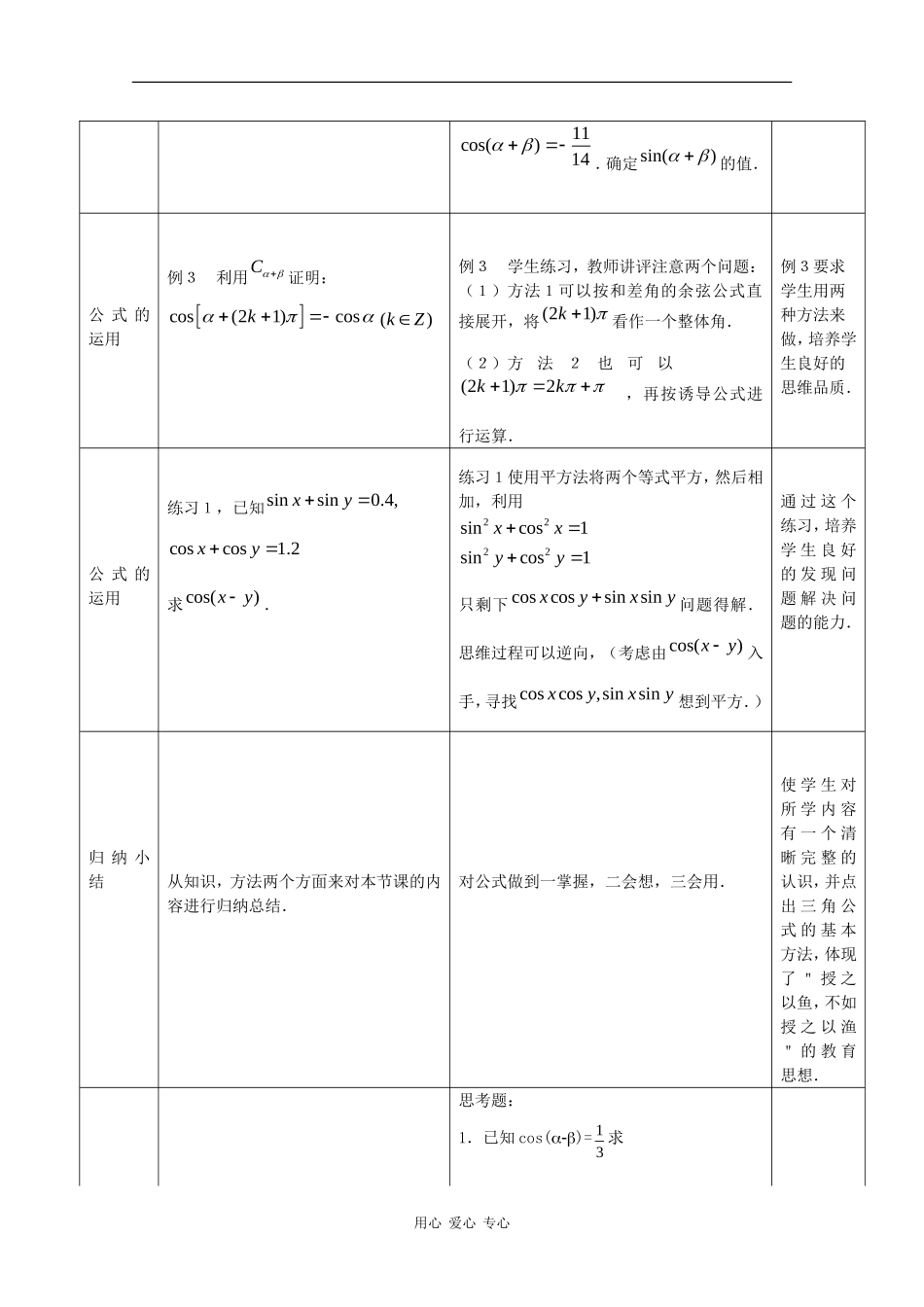
两角和与差的余弦１．知识目标：掌握公式结构特点，会用公式求值．２．能力目标：培养学生的观察，分析，类比，联想能力，间接推理能力，自学能力．３．情感能力：发展学生正向，逆向思维能力，构建良好的数学思维品质．（二）教学重点，难点重点是公式的结构特点，会用公式求值．难点是公式的逆向和变形运用．（三）教学方法教师按照课本的知识结构先设计若干问题，课前印发给学生，引导他们阅读课本，课堂上在教师三导（引导，指导，辅导）下，以学生为主体，对所设问题进行读，议，练，讲，其间教师通过提问，参与讨论，巡视学生练习及板演，观察学生情绪等渠道，及时搜集反馈信息，及时作出评价，再发指令，使教学过程处于动态平衡中．（四）教学过程教学环节教学内容师生互动设计意图复习引入复习公式coscoscossinsincoscoscossinsin先让学生默写两角和与差的余弦公式，然后指出这两个公式是讨论复角与单角,的余弦函数间的关系，且此关系对任意角,均成立，并且要注意coscoscos是错误的．coscoscos以旧引新，注意创设情境，通过设疑，引导学生开展积极的思维活动．用心爱心专心公式的运用例２，已知4cos()52，求cos(),cos()66．例２学生练习，板演，教师讲评注意几个问题：（１）特殊角不需要查表，直接求出三角函数值．（２）再求sin时，要注意角的取值范围，三角函数值的正负．（３）代入时，从左至右依次代入．（４）注意coscossinsincos()coscossinsincos()可以象上面这样逆用．例２是使学生掌握公式的正向应用，并进一步熟悉公式的特征，为后面的灵活运用奠定基础．变式１：已知111coscos()7,14,且,均为锐角，求cos.变式１教师讲评注意几个问题：（１）将看作一个整体，角由()得到．（２）应用公式coscos()cos()cossin()sin（３）由002,2得到0，再进一步参考变式１是一个典型例题，在变式中注意配凑公式，对它的解法深入讨论，有益于启发学生思维，提高学生的解题能力，且在解题过程中提炼思想方法，有利于培养学生良好的思维品质．用心爱心专心11cos()14．确定sin()的值．公式的运用例３利用C证明：cos(21)cosk()kZ例３学生练习，教师讲评注意两个问题：（１）方法１可以按和差角的余弦公式直接展开，将(21)k看作一个整体角．（２）方法２也可以(21)2kk，再按诱导公式进行运算．例３要求学生用两种方法来做，培养学生良好的思维品质．公式的运用练习１，已知sinsin0.4,xycoscos1.2xy求cos()xy．练习１使用平方法将两个等式平方，然后相加，利用2222sincos1sincos1xxyy只剩下coscossinsinxyxy问题得解．思维过程可以逆向，（考虑由cos()xy入手，寻找coscos,sinsinxyxy想到平方．）通过这个练习，培养学生良好的发现问题解决问题的能力．归纳小结从知识，方法两个方面来对本节课的内容进行归纳总结．对公式做到一掌握，二会想，三会用．使学生对所学内容有一个清晰完整的认识，并点出三角公式的基本方法，体现了＂授之以鱼，不如授之以渔＂的教育思想．思考题：1．已知cos()=31求用心爱心专心(sin+sin)2+(cos+cos)2的值。2．sinsin=21，coscos=21，(0,2),(0,2),求cos()的值用心爱心专心