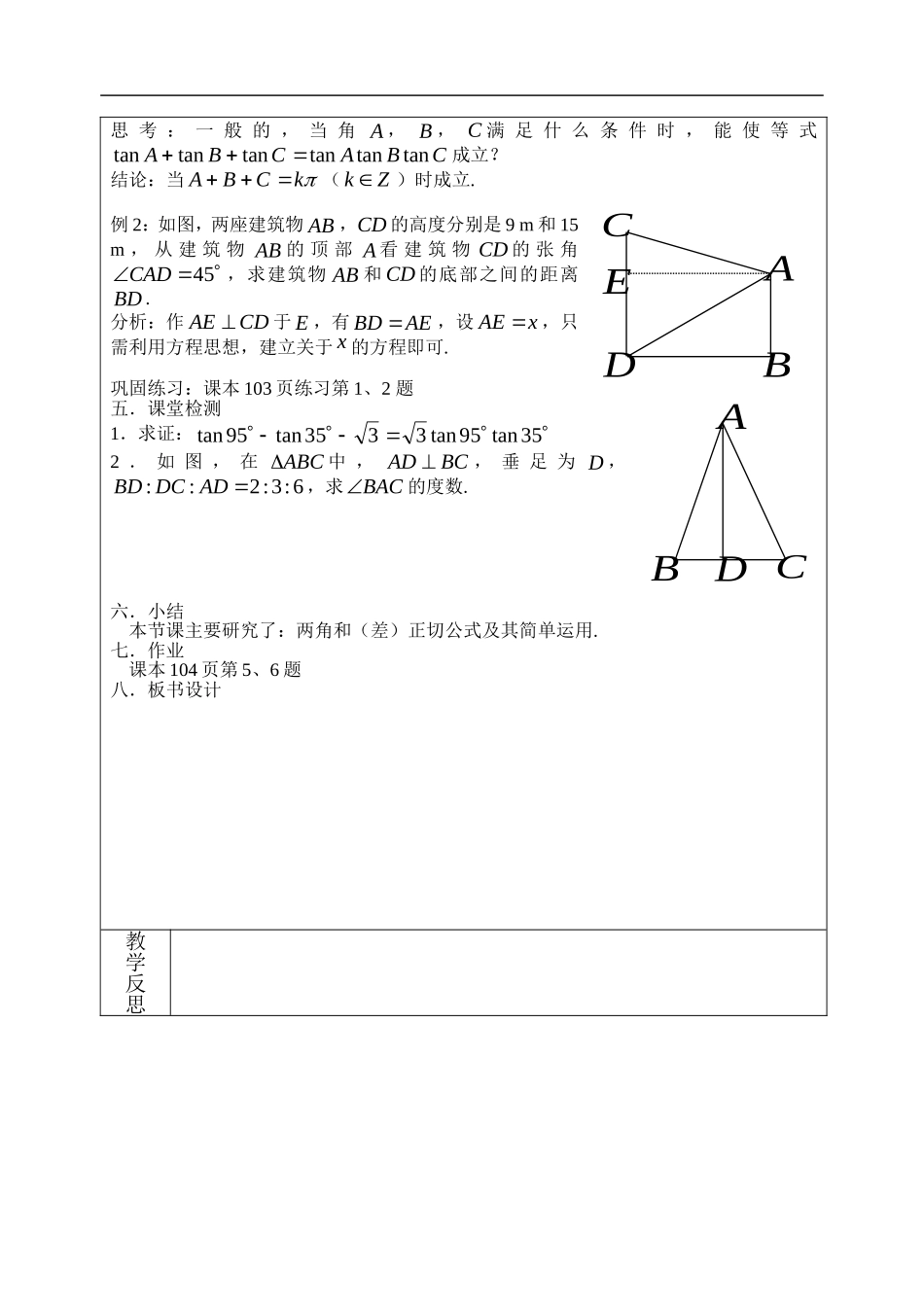
课题两角和与差的正切(二)授课日期课型新授课课时数5三维目标1.进一步掌握两角和与差的正切公式,并从结构上记忆公式;2.能用正切的和差公式进行简单的三角函数式的化简、求值及恒等式证明;3.能用正切的和差公式解决简单的相关的实际问题.教学重点两角和与差的正切教学难点两角和与差的正切公式的运用教学过程:一.课前检测1.求值:(1)1211tan(2)15tan115tan12.已知21tan,求)4tan(.二.新课引入复习回顾两角和与差的正切公式三.目标展示1.进一步掌握两角和与差的正切公式2.能用正切的和差公式进行简单的三角函数式的化简、求值及恒等式证明四.新课教学1.教师活动:以提问形式,让学生复习上节课所学的公式2.学生活动:积极配合老师,思考回答问题3.知识建构:两角和与差的正切公式:tantan1tantan)tan(,()(T)tantan1tantan)tan(.()(T)4.例题讲解例1:在斜三角形ABC中,求证:CBACBAtantantantantantan.分析:待证式与两角和(差)的正切公式比较,都含有正切的和与积,因此可考虑运用两角和的正切公式.思考:一般的,当角A,B,C满足什么条件时,能使等式CBACBAtantantantantantan成立?结论:当kCBA(Zk)时成立.例2:如图,两座建筑物AB,CD的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角45CAD,求建筑物AB和CD的底部之间的距离BD.分析:作CDAE于E,有AEBD,设xAE,只需利用方程思想,建立关于x的方程即可.巩固练习:课本103页练习第1、2题五.课堂检测1.求证:35tan95tan3335tan95tan2.如图,在ABC中,BCAD,垂足为D,6:3:2::ADDCBD,求BAC的度数.六.小结本节课主要研究了:两角和(差)正切公式及其简单运用.七.作业课本104页第5、6题八.板书设计教学反思CEADBBCDA