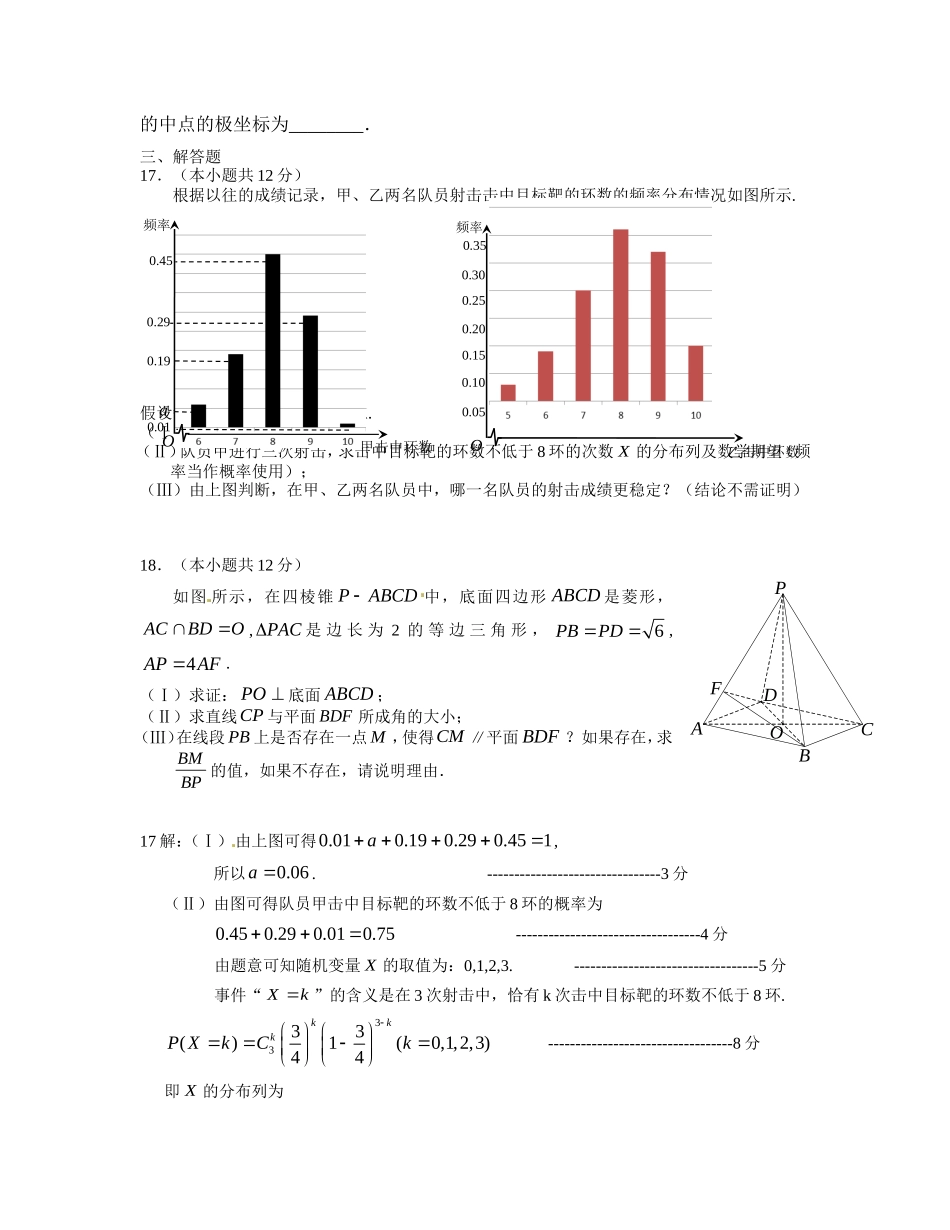
襄阳五中复习训练题(2)命题人杨青林一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知,xyR,i为虚数单位,且(2)1xiyi,则(1)xyi的值为()A.4B.4+4iC.4D.2i2.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB,则集合的真子集共有A.3个B.6个C.7个D.8个3.要得到函数的图象,只要将函数的图象()A.向左平移4单位B.向右平移4单位C.向右平移8单位D.向左平移8单位4.半径为R的球的内接正三棱柱的三个侧面积之和的最大值为()A、B、C、D、5.已知数据是武汉市个普通职工的2013年的年收入设这个数据的中位数为,平均数为,方差为,如果再加上比尔.盖茨的2013年的年收入(约900亿元),则这个数据中,下列说法正确的是()A.年收入平均数大大增大,中位数一定变大,方差可能不变B.年收入平均数大大增大,中位数可能不变,方差变大C.年收入平均数大大增大,中位数可能不变,方差也不变D.年收入平均数可能不变,中位数可能不变,方差可能不变。6.在各项均为正数的等比数列中,,则下列结论中正确的是()A.数列是递增数列;B.数列是递减数列;C.数列既不是递增数列也不是递减数列;D.数列有可能是递增数列也有可能是递减数列.7.已知实数,对于定义在上的函数,有下述命题:①“是奇函数”的充要条件是“函数的图像关于点对称”;②“是偶函数”的充要条件是“函数的图像关于直线对称”;③“是的一个周期”的充要条件是“对任意的,都有”④“函数与的图像关于轴对称”的充要条件是“”其中正确命题的序号是()A.①②B.②③C.①④D.③④8.在边长为1的正三角形ABC中,BD=xBA,CE=yCA,x>0,y>0,且x+y=1,则CD·BE的最大值为()A.-B.-C.-D.-9.设是双曲线的两个焦点,是上一点,若,且的最小内角为,则的渐近线方程为()A.B.C.D.10.已知函数,若1234xxxx,且12()()fxfx34()()fxfx,则12341111xxxx()A.2B.4C.8D.随值变化二.填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分,请将答案填在答题卡的对应题号的位置上,答错位置,书写不清,模棱两可均不得分.(一)必考题(11—14题)11.执行如图所示的程序框图,输出的=.12.若不等式组02(1)1yyxyax表示的平面区域是一个三角形,则a的取值范围是.13.已知椭圆的面积计算公式是,则________;14.设数列这个数列第2010项的值是________;这个数列中,第2010个值为1的项的序号是.(二)选考题(请考生在第15、16两题中任选一题作答,如果全选,则按第15题作答结果计分.)15.(选修4-1:几何证明选讲)如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则2AC+BF·BM=16.(选修4-4:坐标系与参数方程)在极坐标系中,直线ρ(cosθ-sinθ)+2=0被曲线C:ρ=2所截得弦?10nnnSS2的中点的极坐标为________.三、解答题17.(本小题共12分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.假设每名队员每次射击相互独立.(Ⅰ)求上图中a的值;(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数X的分布列及数学期望(频率当作概率使用);(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)18.(本小题共12分)如图所示,在四棱锥PABCD中,底面四边形ABCD是菱形,ACBDO,PAC是边长为2的等边三角形,6PBPD,4APAF.(Ⅰ)求证:PO底面ABCD;(Ⅱ)求直线CP与平面BDF所成角的大小;(Ⅲ)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求BMBP的值,如果不存在,请说明理由.17解:(Ⅰ)由上图可得0.010.190.290.451a,所以0.06a.--------------------------------3分(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为0.450.290.010.75----------------------------------4分由题意可知随机变量X的取值为:0,1,2,3.----------------------------------5分事件“Xk”的...